von Wolfgang Volk

Die Ruine der Franziskaner Klosterkirche gehört zu den heute noch erhaltenen Baudenkmälern der berliner Gründungsgeschichte und ist letztes Zeugnis mittelalterlicher Klosterkultur der Stadt Berlin.

Als erstes vollständig in Backstein ausgeführtes Bauwerk markiert die Klosteranlage des Franziskanerordens den Beginn der regionalen Backsteingotik in Berlin. Nach der Reformation wird der Franzikanerkonvent im 16. Jahrhundert aufgelöst. Es bezieht der Alchemist und kurfürstliche Leibarzt Leonhard Thurneysser das Gebäude und richtet seine Laboratorien, eine Druckerei und eine Bibliothek ein. Noch im selben Jahrhundert gründet sich hier Berlins erstes Gymnasium Zum Grauen Kloster, welches sich zu einer der bedeutendsten Bildungseinrichtungen des Berliner Bürgertums entwickelt.

Gegen Ende des Zweiten Weltkriegs wird die Klosteranlage bei Bombenangriffen stark beschädigt. Erhalten bleibt die Ruine der ehemaligen Klosterkirche, umfasst von einer Grünanlage.¹⁾

Seit den 80er Jahren des vorigen Jahrhunderts wird die Klosterruine kulturell genutzt. So ist vom 19. Mai bis zum 10. Juli 2022 die Ausstellung Prototypical Triangle: Berlin Church Roof Destroyed on April 3, 1945, Reimagined der amerikanischen Künstlerin Alice Adams in der Klosterruine zu sehen. (Das kulturelle Programm und weitere Informationen zur Klosterruine werden im Portal www.klosterruine.berlin kommuniziert.)

Der Begleittext zur Ausstellung lautet: Für ihre erste Einzelausstellung in Deutschland schafft die amerikanische Künstlerin Alice Adams eine raumgreifende, zweiteilige Installation. Inspiration für die Arbeit bietet der Dachstuhl der 1945 zerstörten Klosterkirche. Die stets ortsspezifischen Skulpturen Adams inszenieren die meist unsichtbaren Bedingungen öffentlicher Räume und evozieren in ihrer geisterhaften Theatralirät die verdrängten Dimensionen gesellschaftlichen Zusammenlebens.

Man darf das Kunstobjekt allerdings auch (aus mathematischer Sicht) realistischer betrachten: Der modellierte Teil des Dachstuhls in der Gestalt eines gleichschenkligen Dreiecks setzt sich aus vielen kongruenten Dreiecken zusammen, die zeilenweise angeordnet sind. Etliche scheinen auf dem Kopf (der Spitze) zu stehen.

Bezeichnet man mit n die Anzahl der Zeilen mit den kleinen Dreiecken, so ergeben sich interessante Beziehungen mit sogenannten Dreiecks- und Quadratzahlen [1, S. 4ff]. Für n ≥ 1 ist die n-te Dreieckszahl D_n ist durch die Zuweisung

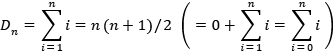
definiert. Es ist bequem, zusätzlich für n = 0 kompatibel D₀ = 0 zu definieren (leere Summe oder die eingeklammerte Variante führen dazu, dass auch D₀ wohldefiniert ist). Man erkennt sofort, dass die Anzahl der „aufrechten“ kleinen Dreiecke mit D_n übereinstimmt. Andererseits stimmt die Anzahl der auf dem Kopf stehenden kleinen Dreiecke mit D_n-1 überein. Diese Beziehungen lassen sich am Kunstwerk von Alice Adams für n=1(1)4 durch Abzählen verifizieren.

Interessanterweise gilt zudem, dass sich die i-te Zeile aus 2·i-1 kleinen Dreiecken zusammensetzt, i-1 auf dem Kopf stehende und i „normal“ orientierte. Nun gilt zudem

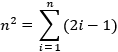
und konsequenterweise demzufolge n² = D_n + D_n-1 .

Diese mathematischen Beziehungen – vorzugsweise durch vollständige Induktion – zu beweisen, sei der Leserin und dem Leser (sofern hinreichend motiviert) anheimgestellt.

¹⁾ Dieser Text (die drei ersten Absätze dieses Beitrags) ist der Informationstafel entnommen, die man links vom Eingangportal der Ruine vorfindet.