Mathematischer Ort des Monats Dezember 2015
Kupfertafeln zur Geschichte der Mathematik
mit Porträts bedeutender Mathematiker sowie ihrer Entdeckungen
in Berlin-Mitte
von
Wolfgang Volk
Der berliner Bildhauer und Grafiker Karl Hillert schuf
die fünf Metallarbeiten, die zusammen ein Ensemble bilden und früher vor dem
Haus der Statistik (siehe auch
diesen Beitrag),
in dem das DDR-Zentralamt für Statistik untergebracht war,
an der Otto-Braun-Straße aufgestellt waren. Früher bedeutet, dass sie
mindestens bis August 2007 noch dort installiert waren, aber bereits im Juni 2008
nicht mehr, sondern - nicht mehr allgemein zugänglich - an der Nordseite des
Bundesministeriums für Arbeit und Soziales (Adresse: Wilhelmstr. 49, 10117 Berlin) platziert sind.
1)
Eine Restauration dieses Kunstwerks wurde im Jahr 2006 unter Federführung der Stiftung Preußischer Kulturbesitz durchgeführt.
Dabei wurden auch zwischenzeitlich entwendete Tafeln und Teile ersetzt. Inzwischen weisen die Kupfertafeln wieder Schäden auf.2)
Da das Kunstwerk eigentlich unzugänglich ist, ist die nachfolgende ausführliche Beschreibung mehr als Dokumentation zu verstehen.
Die obigen Bilder zeigen die Metallarbeiten, so wie sie vor Ort von links nach rechts installiert sind.
Die Bildunterschriften sind kleinen Tafeln entnommen, die neben den einzelnen Objekten an der Hauswand angebracht sind.3)
Die Unterscheidung der beiden Rahmen mit den kleinen Kupfertafeln durch die unterschiedlichen Bezeichnungen erscheint willkürlich,
denn es geht insgesamt um mathematische Entwicklungen vom Altertum bis zur Neuzeit. Die Tafeln unter dem Titel
„Die Entwicklung der Mathematik vom Altertum bis zur Weltraumforschung“ decken den Zeitraum vom Altertum bis zum 17. Jahrhundert ab,
die Tafeln unter dem Schlagwort „Bedeutende Mathematiker mit ihren speziellen mathematischen Entdeckungen“ vom 17. bis ins 20. Jahrhundert.
Bei der Hyperbelkonstruktion sind die beiden Hyperbeläste und die Asymptoten, die Haupt- sowie eine Parallele zur Nebenachse realisiert.
Damit lassen sich auch die Parameter a (halbe Distanz zwischen den Scheitelpunkten) und b (halbe Länge der Parallelen zwischen den Asymptoten)
einfach abmessen. Leider bleibt die Bedeutung der zentralen Kreisscheibe sowie der Geraden und Kreisbogenkonstruktion nicht nachvollziehbar.
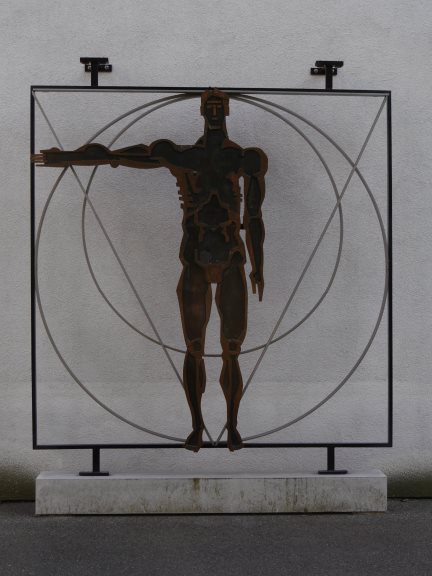
Das Motiv im mittleren Metallrahmen kann als Adaption des
Vitruvianischen Menschen
gedeutet werden.
Bei der Dreieckskonstruktion sind die Dreiecksseiten als durch den äußeren Rahmen materiell begrenzte Geraden realisiert. Ferner sind der Inkreis und die drei Ankreise einbeschrieben.
Während sich der Mittelpunkt des Inkreises als Schnittpunkt der Winkelhalbierenden der Dreieckswinkel ergibt, erhält man die Mittelpunkte der Ankreise als Schnittpunkte der Komplementärwinkel,
die hier zusammen das große Dreieck (der Ankreismittelpunkte) bilden.
Nachstehend werden die Tafeln zu Die Entwicklung der Mathematik vom Altertum bis zur Weltraumforschung wiedergegeben und erläutert:
Auf der linken oberen Tafel (siehe vorstehendes Bild) sind neben den figürlichen Darstellungen in typischer aber auch eigenartiger Kombination aus Profil- und Frontansicht auch die Zahl 404 in
indisch-arabischer, altägyptischer, altgriechischer,
rein additiver römischer und chinesischer Zahlschreibweise wiedergegeben.
Beim nächsten Bild ist der Bildunterschrift kaum noch etwas hinzuzufügen.
Auf der nachstehend abgebildeten Kupfertafel, die sich im Rahmen oben in der Mitte befindet, ist oben das griechische Alphabet vollständig mit Groß- und teilweise in Kleinbuchstaben angegeben.
Die Kleinbuchstaben sind zur Unterscheidung in dunkler Schrift auf hellem Grund dargestellt. Darunter schließt sich eine figürliche Darstellung eines mathematisch-philosophischen Zirkels(?) mit folgendem Text an:
„In der Mathematik haben die alten Griechen mit Beweisen operiert. Dadurch wurde sie zur Wissenschaft.“
(Die Satzenden sind nicht durch einen Punkt realisiert, sondern die betreffenden Zeilen sind mit kleinen Quadraten aufgefüllt.)
Die Tafel rechts oben im Metallrahmen zeigt ein Porträt von
Albrecht Dürer. Dieses wird oben auf der linken Seite vom Geburts- und vom Sterbejahr (1471 und 1528) flankiert, rechts von seinem bekannten Monogramm.
Unter dem Porträt sind der durch „A.“ und der Zuname zusammen mit den drei Worten „Harmonielehre“, „Proportionslehre.“ und „Perspektivlehre“ wiedergegeben.
Dies dürfte eine Referenz an das Buch A. Dürers Unterweisung der Messung, erschienen in Nürnberg im Jahr 1525 sein (vergleiche
Dürer als Mathematiker).
Die mit dem Porträt angesprochenen Schlagworte erfahren ihre Manifestation mit dem Inhalt der Tafel “Proportionsstudie von Albrecht Dürer“. Da lässt sich ein Bogen zu den alten ägyptern spannen,
die für ihre Reliefs bereits mithilfe eines Quadratnetzes Proportionen des menschlichen Körpers festlegten (siehe [1, S. 21 f.]).
Die mit der nachstehenden Tafel dargestellte Anwendung bezieht sich auf die Frage bis zu welcher Entfernung d vom Meeresufer aus man ein Schiff, dessen Masthöhe bekannt ist, sehen kann. Dabei werden die Refraktion und die Augenhöhe über dem Meeresspiegel vernachlässigt.
Im Erdmittelpunkt ist zusätzlich die Figur zum Lehrsatz eingezeichnet. Ferner sind die Längen R für den Erdradius, h für die Höhe des Schiffs und d in die Grafik eingetragen. Darunter sind die Gleichungen:
(R + h)2 = R2 + d2
und daraus abgeleitet
2Rh + h2 = d2
angegeben.
(R + h)2 = R2 + d2
und daraus abgeleitet
2Rh + h2 = d2
angegeben.
Die Kupfertafel links unten zeigt ein Porträt von
Adam Ries(e) aus Staffelstein im Fränkischen (nördlich von Bamberg), der im sächsischen Annaberg als Rechenmeister tätig war. Heute ist sein
Wohnhaus mit seiner Rechenschule in Annaberg ein Museum. Bekannt wurde er durch sein Rechenbuch Rechnung
auff den Linihen vnd Feder, das in über 120 Auflagen erschien, und seinem Algebra-Lehrbuch Coß, das allerdings nie gedruckt wurde.
Links neben dem Porträt sind Geburts- und Sterbejahr, 1492 und 1559, angegeben und rechts ein Rechenschema für die sogenannte Neunerprobe
(siehe auch [2, S. 67 ff.]).
Und weil das Porträt von A. Ries unmittelbar unterhalb der Anwendung des Satzes des Pythagoras benachbart ist, soll hier ein Gedicht zitiert werden, das beide verbindet (einschließlich des einführenden Absatzes aus [3, S. 62 f.]):
In vielen Auflagen der „Ziffernrechnung“ schickt Ries - ähnlich wie andere Autoren von Rechenbüchern auch - als „ Hinwendung an den Leser“ ein Gedicht voraus, das, in der tiefen überzeugung wurzelnd,
Gott habe alles nach Maß, Gewicht und Zahl geordnet, den Leser zum Erlernen der Rechenkunst motivieren soll. (Hinweis: Das Gedicht ist in der Sprache der damaligen Zeit verfasst, aber der Inhalt durchaus für jemanden, der der deutschen Sprache mächtig ist,
verständlich und bereit ist, ein „v“ auch für ein „u“ zu lesen und ggf. eine Dehnung einzufügen.)
PYTHAGORAS der sagt für war /
All Ding durch zal werd offenbar /
Drumb sih mich an / verschmeh mich nit /
Durchliß mich vor / das ich dich bitt /
Vnd merck zum anfang meine lehr /
Zu Rechenßkunst dadurch dich ker /
In Zal / in Maß / vnd in Gewicht /
All Ding von Gott sind zugericht.
Klerlichen Salomon das sagt /
Ohn Zal / ohn Maß / Gott nichts behagt /
Beschreibt Vns auch S. Augustin /
Vnd malet Vns frey in den Sinn.
Sich sol kein Mensch nichts Vnterstehn /
Kein Göttlich / weltlich Kunst begehn
Ohn Rechnen art / durch ware Zal /
Bewert ist das in manchem fall.
Ein Mensch dem Zal verborgen ist /
Leichtlich verfüret wird mit list.
Dis nim zu hertzen / bitt ich sehr /
Vnd jeder sein Kind Rechnen lehr /
Wie sichs gegen Gott Vnd Welt verhalt /
So werden wir in ehren alt.
All Ding durch zal werd offenbar /
Drumb sih mich an / verschmeh mich nit /
Durchliß mich vor / das ich dich bitt /
Vnd merck zum anfang meine lehr /
Zu Rechenßkunst dadurch dich ker /
In Zal / in Maß / vnd in Gewicht /
All Ding von Gott sind zugericht.
Klerlichen Salomon das sagt /
Ohn Zal / ohn Maß / Gott nichts behagt /
Beschreibt Vns auch S. Augustin /
Vnd malet Vns frey in den Sinn.
Sich sol kein Mensch nichts Vnterstehn /
Kein Göttlich / weltlich Kunst begehn
Ohn Rechnen art / durch ware Zal /
Bewert ist das in manchem fall.
Ein Mensch dem Zal verborgen ist /
Leichtlich verfüret wird mit list.
Dis nim zu hertzen / bitt ich sehr /
Vnd jeder sein Kind Rechnen lehr /
Wie sichs gegen Gott Vnd Welt verhalt /
So werden wir in ehren alt.
Die nachstehend abgebildete Tafel zeigt die Abhängigkeit der Flugbahnen und der Wurfweite eines kugelförmigen
Körpers in Abhängigkeit vom Winkel zur Horizontalen. G. Galilei hat Versuche zum freien Fall durchgeführt
und auch die Wurfbewegung untersucht. Der auf der Tafel nur schwer lesbare Text ist als Bildunterschrift angegeben.
Unmittelbar rechts daneben findet man auf einer weiteren Kupfertafel ein Porträt von
Galileo Galilei. Am linken Rand ist der Name von unten
lesbar wiedergegeben, in der rechten unteren Ecke das Geburts- und das Sterbejahr, 1562 und 1642. Dabei ist zu beachten,
dass die letzte Jahreszahl bereits gemäß des
Gregorianischen Kalenders angegeben ist.
Die Kupfertafel in der rechten unteren Ecke zeigt das Porträt des französischen Mathematikers Blaise Pascal.
Auf der Tafel schräg darüber ist die von ihm entwickelte Additions- und Subtraktionsmaschine abgebildet,
die später Pascaline genannt wurde.
Im Mathematisch-Physikalischen Salon Dresdens ist ein Exemplar dieser Rechenmaschine ausgestellt.
Auf der Tafel ist folgender Text zu lesen:
Mechanische Rechenmaschine 1642
von Blaise Pascal konstruiert
von Blaise Pascal konstruiert
Das Porträt B. Pascals ist mit dem Namen überschrieben. Im Hintergrund ist eine geometrische Figur zu erkennen, die den sogenannten
Satz von Pascal illustriert.
Darunter sind wieder Geburts- und Sterbejahr, 1623 und 1662 genannt.
Nachfolgend werden die Tafeln zu Bedeutende Mathematiker mit ihren speziellen mathematischen Entdeckungen dokumentiert:
Die Tafel oben links in diesem Metallrahmen zeigt eine Skizze der
Rechenmaschine, die G. W. Leibniz konstruierte.
Sie war darauf angelegt, dass man mit ihr nicht nur addieren und subtrahieren konnte, sondern auch multiplizieren und dividieren (sogenannte 4-Spezies-Rechenmaschine).
(Mithilfe eines speziellen Algorithmus' können auch Wurzeln gezogen werden!)
Unterhalb der Darstellung der Rechenmaschine und dem Text, der vorstehend als Bildlegende wiedergegeben ist, ist eine Matrix aus kleinen Quadraten dargestellt. Etwa ein Drittel der Quadrate ist durch den folgenden Text ersetzt:
1697 stellte
G. W. Leibniz
das
Binär-Zählsystem
auf.
Es bildet
die Voraussetzung
für das
maschinelle
Rechnen.
G. W. Leibniz
das
Binär-Zählsystem
auf.
Es bildet
die Voraussetzung
für das
maschinelle
Rechnen.
Das nachstehende Porträt von Gottfried Wilhelm Leibniz wird oben rechts von Geburts- und Sterbejahr, 1646 und 1716, flankiert
und unten vom Namen, wobei von den Vornamen nur die Initialen angegeben sind.
Die nächste vorzustellende Tafel kommt völlig ohne Text daher. Sie zeigt - ohne dass es für diese Interpretation eine Rechtfertigung gäbe - die Erde mit elliptischen Satellitenbahnen und futuristisch anmutenden Raumstationen.
Diese Tafel ist aber sicher eine auf den Raketenpionier
Konstantin Eduardowitsch Ziolkowski gerichtete Referenz.
Das Porträt von Konstantin Eduardowitsch Ziolkowski wird nicht nur vom Namen (mit abgekürzten Vornamen und den Lebensdaten [1857 - 1935]) ergänzt, sondern darüber hinaus mit drei Formeln,
die hier nicht näher erläutert werden können, aber mit der Raketengrundgleichung in Beziehung stehen dürften:
V =V1 ln (1 + M2 / M1 )
V =V1 ln (1 + M2 / M1 ) ( ( p-g)/p )
M2 = M1 [ ℓ ( T1 p ) 1/2 / T2(p-g) 1 ]
V =V1 ln (1 + M2 / M1 ) ( ( p-g)/p )
M2 = M1 [ ℓ ( T1 p ) 1/2 / T2(p-g) 1 ]
Auch das Porträt von Isaac Newton ist mit dem Namen und dem Geburts- und Sterbejahr, 1643 und 1727, überschrieben.
Darüber hinaus ist noch folgende Gleichung
(Δx)2 + (Δy)2 + (Δz)2 + (Δt)2 = (ΔL)2
angegeben. Hier zeigt sich die Problematik, wenn Gleichungen ohne Beschreibung der Bedeutung der Variablen angegeben werden.
x, y und z werden wohl Raumkoordinaten sein, t könnte etwas mit der Zeit zu tun haben, wird aber erst durch Multiplikation mit einer Geschwindigkeit (von Licht?) zu einer Größe,
die eine sinnvolle Interpretation, nämlich die Anwendung des Pythagoräischen Lehrsatzes in vier Dimensionen, zulässt.
Die unter dem Porträt platzierte Kupfertafel soll einen Auszug aus I. Newtons Werk
Philosophiae Naturalis Principia Mathematica, oft - wie auch hier - nur als Principia bezeichnet, wiedergeben.
In diesem Buch sucht man diese Grafik allerdings vergebens. Auch muss man der Bildunterschrift „Ellipsenbahn der Planeten“ misstrauen.
Wie bei den anderen Porträts, sind hier beim Bildnis Leonhard Eulers auch der Name des Porträtierten und das Geburts- und das Sterbejahr, 1707 und 1783, angegeben.
Diese Tafel ist in der untersten Reihe ganz links angebracht.
Rechts neben dem Porträt ist eine kleinere Tafel, worauf eine Kugel mit drei Großkreisen und dem eingebetteten sphärischen Dreieck dargestellt sind. Darüber ist die Bezeichnung
Eulersche Dreiecke zu lesen. Eulersche Dreiecke zeichnen sich gegenüber allgemeinen sphärischen Dreiecken dadurch aus,
dass die Innenwinkel allesamt kleiner als 180° sind und damit die Dreiecksfläche kleiner als die halbe Kugeloberfläche ist.
Auf dem Porträt von Carl Friedrich Gauß ist oben links ein Polygon teilweise zu sehen. Dieses stellt ein regelmäßiges 17-Eck dar,
von dem C. F. Gauß zeigte, das es sich ausschließlich mit Zirkel und Lineal konstruieren lässt.
Darunter sind die Gleichung
xn - 1 = 0 ,
der Name und die Lebensdaten, 1777 - 1855, angegeben. Dieses Porträt zierte in den Jahren 1991 bis 2001 die Vorderseite der
10-DM-Banknote.
Auf der nächsten Tafel ist eine Teilansicht eines
Kernspeichers mit Ferritringen wiedergegeben, eine mittlerweile völlig antiquierte Computer-Technologie.
Ferrit kann in zwei Richtungen magnetisiert werden, also die Information einer Binärstelle (Bit) speichern. Damit wird wieder ein Bogen zu Leibniz' Binärzählsystem (siehe oben) geschlagen.
Mit der letzten Kupfertafel wird
Albert Einstein gewürdigt, wobei dieser Tage der 100. Jahrestag der Veröffentlichung seiner
Allgemeinen Relativitätstheorie begangen wird. Unter dem Porträt sind die Lebensdaten, 1879 und 1955, sowie der Name eingraviert.
Referenzen
| [1] | Hans Strelocke: Ägypten und Sinai, DuMont Kunst-Reiseführer, 13. veränderte Aufl., DuMont Buchverlag, Köln, 1986 | |
| [2] | Hans Wußing: Adam Ries, (erschienen in der Reihe: Biographien hervorragender Naturwissenschaftler, Techniker und Mediziner, Bd. 95), Springer Fachmedien, Wiesbaden, 1989, urspr. ersch. bei BSB B. G. Teubner, Leipzig, 1989, ISBN 978-3-00687-5 | |
| [3] | Hans Wußing: Adam Ries, 2. durchgesehene und erw. Aufl., B. G. Teubner, Leipzig, und vdf Verlag der Fachvereine an den schweizerischen Hochschulen und Techniken, Zürich, 1992, ISBN 3-8154-2500-X (Teubner), ISBN 3-7281-1923-7 (vdf) |
Bildnachweis
| alle Bilder | Wolfgang Volk, Berlin, aufgenommen am 30. August 2015 |
1) Beim Tag der offenen Tür der Bundesministerien im Jahr 2014 nahm der Autor an einer Führung
durch das Bundesministerium für Arbeit und Soziales teil. Es gelang dem Mitarbeiter, der die Führung durchführte, auf meine
Frage hin herauszubekommen, dass und wo das Werk von K. Hillert aufgestellt ist. Man führte mich durch den für die
allgemeine öffentlichkeit nicht zugängliche Kantine zum nördlichen Hinterausgang, wo das
Werk von K. Hillert installiert ist. Der Rückweg ist nur mit Schlüsselgewalt möglich.
Beim anschließenden Besuch des benachbarten Bundesministeriums für Ernährung und Landwirtschaft konnte die Installation der fünf Metallarbeiten problemlos in Augenschein genommen werden.
Anders beim Offenen Tag 2015 am 30. August. Da wurde dem Autor zunächst der Zugang durch das Wachpersonal verweigert. Durch Ansprache des Verantwortlichen der Wachmannschaft war es dann möglich, die Fotografien, die auf dieser Seite wiedergegeben werden, unter Aufsicht aufzunehmen.
Beim anschließenden Besuch des benachbarten Bundesministeriums für Ernährung und Landwirtschaft konnte die Installation der fünf Metallarbeiten problemlos in Augenschein genommen werden.
Anders beim Offenen Tag 2015 am 30. August. Da wurde dem Autor zunächst der Zugang durch das Wachpersonal verweigert. Durch Ansprache des Verantwortlichen der Wachmannschaft war es dann möglich, die Fotografien, die auf dieser Seite wiedergegeben werden, unter Aufsicht aufzunehmen.
2) Die Wiederherstellung der Tafeln erfolgte teilweise auf der Grundlage der Fotonegative des Autors, die im Artikel
Kupfertafeln mit Porträts namhafter Mathematiker
wiedergegeben werden. Der Artikel
Tafeln zu Albrecht Dürer, Leonhard Euler, Galileo Galilei, Carl Friedrich Gauß,
Gottfried Wilhelm Leibniz, Isaac Newton, Blaise Pascal and Adam Ries(e) in Berlin (Deutschland) wird ein Teil
der Kupfertafeln nach der Restauration gezeigt. Ein Vergleich mit den aktuellen Aufnahmen zeigt, dass die Tafeln wieder
gelitten haben.
3) Die kleinen Tafeln weisen den Namen des Künstlers in größerer fetter Schrift aus, darunter folgen jeweils der Text,
der oben als Bildunterschrift angegeben ist, und darunter die Bezeichnung „Metallgestaltung“ aus.
Außerdem ist in diesem Zusammenhang auf zwei Sachverhalte hinzuweisen:
a) Statt korrekterweise „Ankreiskonstruktion“ ist auf dem Schild „Anreißkonstruktion“ zu lesen.
b) Die beschreibenden Schilder sind in der falschen Reihenfolge angebracht.
a) Statt korrekterweise „Ankreiskonstruktion“ ist auf dem Schild „Anreißkonstruktion“ zu lesen.
b) Die beschreibenden Schilder sind in der falschen Reihenfolge angebracht.