von Wolfgang Volk

Auf dem Heinrich-Dathe-Platz, unmittelbar am U-Bahnhof Tierpark in Berlin-Friedrichsfelde gelegen, ist ein Lage- und Höhenfestpunkt auf einem Steinquader markiert (siehe nachstehendes Bild). In einem gewissen Abstand stehen in einem Viertelkreis vier weitere, oben abgeschrägte Stelen, die Metallplatten mit Skizzen zu geodätischen Sachverhalten zeigen. Das ganze Ensemble ist auf obigem Bild zu sehen. (Die Blickrichtung ist etwa gen Westen.)

Allerdings handelt es sich bei diesem Lage- und Höhenfestpunkt um ein technisches Denkmal; der Punkt selbst ist nicht Teil des Festpunktnetzes Berlins und die Zahlenwerte nicht mit der erforderlichen Genauigkeit ermittelt.

Die Marke auf der zentralen quaderförmigen Säule ist mit dem Text „Messungspunkt“ versehen (vergleiche nachstehendes Bild). Eine Metallplakette weist darauf hin, dass es sich um einen Lage- und Höhenfestpunkt handelt.

Die oben auf dem ersten Bild am weitesten links stehende Stele zeigt lediglich eine schlichte Windrose, bei der die vier Haupthimmelsrichtungen mit den Buchstaben „N“ für Nord, „O“ für Ost, „S“ für Süd und „W“ für West ausgezeichnet sind.

Die nächste Stele gegen den Uhrzeigersinn – also nach rechts auf dem ersten Bild auf dieser Seite – zeigt die im Zusammenhang mit Höhenangaben beteiligten Flächen.

Von oben nach unten sind dies

• die (physikalische) Erdoberfläche, auf der auch die Punkte liegen, deren Höhen zu bestimmen sind,
• die durch die Landmasse fortgesetzte Meeresoberfläche, das Geoid (hier fälschlicherweise Quasigeoid genannt) und
• das als rechnerische Bezugsfläche verwendete (Erd-)Ellipsoid.

Es ist gut dargestellt, dass durch die unregelmäßige Massenverteilung alle Linien – wie die Linien der Schwerkraft – und bis auf das (Rotations-)Ellipsoid auch alle Flächen unregelmäßig gekrümmt sind. Die Normalhöhe (NHN) eines Punktes ist sein Abstand vom Geoid (gemessen entlang der Schwerelinie durch diesen Punkt, die Schwerelinien stehen stets senkrecht auf der – Geoid genannten – Niveaufläche).

Der bisher beschriebene Inhalt dieser Tafel wird durch folgenden Text komplettiert: (Diese Höhenangabe ist definitiv nicht exakt, üblicherweise wird sie für echte Höhenfestpunkte mit Millimeter-Genauigkeit angegeben; außerdem werden Festpunkte nicht konstruiert, sondern gemäß Sicherheitsaspekten vermarkt und die Werte gemessen bzw. aus genau gemessenen Bestimmungsgrößen berechnet.)

Der Zusammenhang von Erdellipsoid, Geoid und Quasigeoid soll weiter unten, nach der Beschreibung der beiden noch verbleibenden Tafeln, erläutert werden.

In der Antike und auch in der Zeit danach nahm man für den Planeten Erde eine Kugelgestalt an (1. Näherung). Man denke dabei an Aristoteles (384 v. Chr. – 322 v. Chr.) (siehe insbesondere der Wikipedia-Artikel zur flachen Erde) und Eratosthenes (zwischen 276 und 273 v. Chr. – 194 v. Chr). Aber spätestens seit Isaac Newton (1642 – 1726) ahnte man, dass die Erde an den Polen abgeflacht sein müsse (siehe den Wikipedia-Artikel zum Referenzellipsoid). Dabei standen aber aus (guten) physikalischen Gründen immer nur Rotationsellipsoide zur Debatte, d. h. die beiden Halbachsen in der Äquatorebene sind gleich groß, nur die Länge der halben Rotationsachse weicht davon ab.

So hat die französische Akademie der Wissenschaften verfügt, dass zwei Expeditionen zur Längenbestimmung von Meridianbögen unternommen werden, eine nach Südamerika unter der Leitung von Pierre Bouguer und Charles Marie de la Condamine und eine nach Lappland unter der Leitung von Pierre Louis Moreau de Maupertuis. Die Vermessungsarbeiten in Südamerika dauerten von 1736 bis 1739, die in Lappland von 1736 bis 1737, ihre Auswertung ergab zweifelsfrei eine Abplattung an den Polen (2. Näherung).

Eine der ersten Bestimmungen des Erdellipsoids gelang Friedrich Wilhelm Bessel im Jahr 1841. Die Bedeutung und die damit einhergehende Rechtfertigung, auf der Plakette der vorletzten Stele das sogenannte Bessel-Ellipsoid zu erwähnen, rührt daher, dass es bis in unsere Zeit die Grundlage für die in Deutschland verwendeten Koordinatensysteme bildet (dazu noch mehr in den nachstehenden Betrachtungen).

Die Arbeitsweise mit so einem Erdellipsoid ist wie folgt: Seine Oberfläche wird als Erdoberfläche angenommen und die Flächennormale als empfundene Lotrichtung. Damit ist die geografische Breite eines Ortes genau der Winkel zwischen dieser Lotrichtung und der Äquatorebene, wobei jedem sofort auffallen dürfte, dass dies kein exakter Ansatz sein kann, da das Lot im Allgemeinen nicht durch den Erdmittelpunkt (Schwerpunkt des Erdellipsoids) führt (außer am Äquator und an den beiden Polen). Dieser Ansatz ist jedoch vernünftig, präsentiert sich doch die wahrgenommene Erdgestalt als achsensymmetrisch gekrümmte Fläche und die Lotrichtung schon ganz gut mit der perönlich wahrgenommenen Schwerelinie (Lot im Standpunkt).

Auch wenn sich das Modell der ellipsoidalen Gestalt der Erdkugel aus mathematischer Sicht akzeptabel anfühlt, sollte es doch nicht unerwähnt bleiben, dass für geodätische Berechnungen in der Regel keine geschlossenen Formeln zur Verfügung stehen, sondern Reihenentwicklungen zur Anwendung kommen.

Neben dem abgebildeten Ellipsoid mit Gradnetz ist auf dieser Tafel noch folgender Text zu lesen: (Die geografischen Koordinaten sind mit einer Genauigkeit von einer Nachkommastelle der Winkelsekunden angegeben. Dies entspricht einer Lagegenauigkeit von etwa 3 m.)

Mit den bisher entwickelten Überlegungen glaubt man, mit einem Rotationsellipsoid ein zumindest aus mathematischer Sicht hinreichend genaues Umfeld gefunden zu haben. Trotzdem nimmt man als Individuum die nähere Umgebung auf der Erde als Ebene wahr. Da ist natürlich für die Berechnung von Streckenlängen und Flächeninhalten ein kartesisches Koordinatensystem das Mittel der Wahl.

Damit ist man auch mitten in der Diskussion zum Thema Kartenprojektionen, die hier natürlich nicht in ihrer ganzen Tiefe geführt werden kann. Aber am Anfang der für die im Zusammenhang mit dem Lage- und Höhenfestpunkt relevanten, auf den Stelen präsentierten Sachverhalten stehen die Überlegungen des Kosmografen Gerhard Kremer (1512 – 1594, in der latinisierten Form besser bekannt als Gerhardus Mercator) im Vordergrund.

Das Verdienst von Gerhard Mercator – das dürfte der Name sein, unter dem er am bekanntesten ist – ist die Entwicklung einer winkeltreuen Abbildung von der Erdkugel auf einen (mathematischen) Zylinder, dessen Achse mit der Rotationsachse der Erde übereinstimmt. Die Landkarte und dmit auch ein kartesisches Koordinatensystem erhält man dann durch Aufschneiden und Abrollen der Zylinderoberfläche. Das Ergebnis sind die globalen Landkarten, bei denen Grönland und Afrika annähernd gleichgroß wiedergegeben werden (siehe das nachstehende Bild).

Er hat für die verschiedenen Werte der geografischen Breite φ das Integral 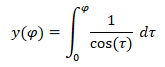rechnerisch bestimmt. Das Besondere dabei: Die Infinitesimalrechnung von Gottfried Wilhelm Leibniz und Isaac Newton war zu diesem Zeitpunkt noch gar nicht entwickelt. Zusammen mit der Formel (alle Winkel im Bogenmaß) 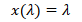erhält man die Lage von Punkten auf der Karte, versehen mit einem kartesischen Koordinatensystem, anhand ihrer geografischen Koordinaten (auf der Erdkugel). Wie gesagt ist diese Projektion winkeltreu, man erkennt aber sofort, dass Längen und Flächeninhalte nur in Äquatornähe akzeptabel wiedergegeben werden.

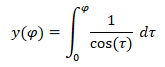
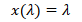
Die Idee keinen Zylinder wie von Gerhard Mercator in normaler Lage (senkrecht) zu verwenden, sondern in transversaler Lage (Zylinderachse waagrecht, in der Äquatorebene verlaufend) geht wohl auf Johann Heinrich Lambert zurück. Carl Friedrich Gauß favorisierte einen elliptischen Zylinder, der das Erdellipsoid in einem Meridian berührt, und Louis Krüger arbeitete die Gedanken weiter aus und war an der Einführung der sogenannten Gauß-Krüger-Koordinatensysteme beteiligt. Dabei wird jeweils nur ein 3°-breiter Meridianstreifen winkeltreu auf einen elliptischen Zylinder abgebildet und jeder dieser Meridianstreifen mit einer Kennziffer (Zählweise vom Nullmeridian, durch Greenwich) versehen. Auf diese Weise erhält man eine Reihe kartesischer Koordinatensysteme, nicht nur für die Produktion von Landkarten, sondern auch als Berechnungsgrundlage für das Liegenschaftskataster.

UTM-Koordinatensysteme basieren auf den gleichen Ideen wie Gauß-Krüger-Koordinatensysteme. Dabei werden jedoch 6°-breite Meridianstreifen verwendet und eine Längenreduktion von 0,04% vorgenommen. Dies kann dahingehend interpretiert werden, dass der elliptische Zylinder das Erdellipsoid schneidet. Mit diesen Informationen ist die grafische Darstellung auf der letzten Stele zu verstehen.

Ergänzend sei noch darauf hingewiesen, dass UTM auf dem Referenzellipsoid GRS80 (Geodätisches Referenzsystem 1980) bzw. WGS84 (World Geodetic System) basiert.

Auf der Metalltafel ist folgender Text zu lesen: Aus dem Rechtswert lässt sich bereits ablesen, dass der Festpunkt im 33. UTM-Meridianstreifen (von der Datumsgrenze aus nummeriert) und etwa 5817 km nördlich des Äquators liegt. Auf ETRS 89 soll hier nicht weiter eingegangen werden, da dies für den allgemeinen Überblick nicht zwingend erforderlich ist.

Wie weiter oben bereits versprochen, soll noch der Zusammenhang von Erdellipsoid, Geoid und Quasigeoid erläutert werden.

Das Geoid darf man sich als die Niveaufläche des Meeresspiegels vorstellen, fortgesetzt in den Landmassen. Damit ist das Geoid nur auf den Weltmeeren näherungsweise erfahrbar und, da sich der überwiegende Teil der Landmassen über dem Meeresspiegel befindet, sonst nicht (für Messungen) zugänglich. Die Gestalt des Geoids als Bezugsfläche im Schwerefeld der Erde ist von der Massenverteilung abhängig und damit nicht mit Formeln mathematisch zu beschreiben. Jedoch lässt sich durch Satellitenbeobachtungen, so wie sie auch am Geoforschungszentrum in Potsdam durchgeführt werden, in gewisser Weise rekonstrieren. Das Ergebnis dieser Arbeiten ist eine unregelmäßige Figur, die als Potsdamer Kartoffel bezeichnet wird. Die Abweichungen zwischen Geoid und dem Referenzellipsoid WGS84 werden mit maximal ±40 m beziffert.

Das Quasigeoid ist der Versuch einer Rekonstruktion des Geoids aus gemessenen Geländehöhen und idealisierten Annahmen der Lotrichtungen (Flächennormale des Referenzellipsoids). Es besitzt für die vorstehenden Ausführungen kaum Relevanz, außer im Zusammenhang mit der Umstellung des Höhensystems von Normalnull (NN) auf Normalhöhennull (NHN) bei dem das Schwerefeld der Erde mit berücksichtigt wird (vergleiche auch die Höhenangabe auf der zweiten Tafel). Für weitere Details sei auf die nachstehenden Wikipedia-Artikel verwiesen:

• Höhe (Geodäsie)
• Normalhöhennull und
• Deutsches Haupthöhennetz