Beitrag vom Januar 2019
Zeitzeugnis zu Berliner Spuren zum Max-Planck-Institut für Mathematik und
zur Fields-Medaille 2018
Persönliche Begegnungen im Zusammenhang neuerer Ereignisse
Zusammenfassung
Einer der Kodirektoren des
Max-Planck-Instituts für Mathematik (MPIM) in Bonn,
Peter Scholze,
wurde im August 2018 auf dem
Internationalen Mathematiker-Kongress (ICM)
in Rio de Janeiro mit einer Fields-Medaille ausgezeichnet.
Sie zählt soviel wie der Nobelpreis in anderen Wissenschaftsdisziplinen.
Es ist das zweite Mal, dass dieser Preis nach Deutschland ging.
Erster deutscher Preisträger war 1986
Gerd Faltings,
der danach auch Kodirektor des MPIM wurde.
Ihn lernte ich persönlich vor 1986 kennen, traf ihn danach auf einigen Tagungen.
Später wurde auch
Juri Manin Kodirektor des MPIM.
Er hatte mir etliche Jahre zuvor in Berlin und in Moskau gute Tipps für meine Arbeit gegeben,
die unter anderem in die allererste
Euler-Vorlesung mündete.
Ich durfte sie am Karl-Weierstrass-Institut im Akademie-Gebäude gegenüber dem
Gendarmenmarkt in Berlin-Mitte halten. Nach der Abwicklung der
Akademie der
Wissenschaften der DDR im Jahr 1991 wurde ich beim MPIM geparkt (und alimentiert)
bis ein Lehrstuhl für mich in Berlin frei wurde.
Rückblickend steht fest, dass das mathematisch-orientierte
Heinrich-Hertz-Gymnasium in Berlin sowohl für
Peter Scholze wie auch seinem langjährigen Betreuer
Michael Rapoport
eine wichtige Rolle spielte. Eine große Kraft steckte schon in der Ausrichtung der Schule in
den 1960er Jahren auf die Mathemtik. Die Hauptinitiatoren waren meine Lehrer
Hans Reichardt und
Heinrich Grell an der
Humboldt-Universität.
Die Kontaktliste der beiden Initiatoren enthält so große Namen wie:
Hieraus ist die große Energie erklärlich mit der Reichardt und Grell
Gründung und Arbeit des Heinrich-Hertz-Gymnasiums verfolgten.
Die Wucht mathematischer Leistungen des 20. Jahrhunderts wurde somit über Berlin
weitergetragen bis zur Fields-Medaille 2018.
Inhaltsverzeichnis
- Einführung
- Kurt Hensel
- Kurze Biographie
- Persönlich-Familiäres
- Wissenschaftliche Leistung
- Meine Berührungspunkte
- Helmut Hasse
- Kurze Biographie
- Wissenschaftliche Leistung
- Meine Berührungspunkte
- Hans Reichardt
- Kurze Biographie
- Wissenschaftliche und organisatorische Leistungen
- Meine Berührungspunkte
- Emmy Noether
- Kurze Biographie
- Heinrich Grell
- Kurze Biographie
- Meine Berührungspunkte
- Wissenschaftlich-organisatorische Leistungen
- Die Budachsche Jugend-Forschungsgruppe
- Die Rapoports
- Die Eltern
- Michael Rapoport
- Das Heinrich-Hertz-Gymnasium
- Namhafte Absolventen
- Kritische Bemerkung zur Schulchronik
- Zum Gründungsdirektor des MPIM Friedrich Hirzebruch (1927-2012)
- Juri Iwanowich Manin (*1937)
- Gerd Faltings
- Peter Scholze
- Wissenschaftliche Biographie
- Auf dem Weg zur Fields-Medaille 2018
- Pressestimmen im August 2018
- Echo einiger internationaler Kollegen
- Bildnachweis
Einführung
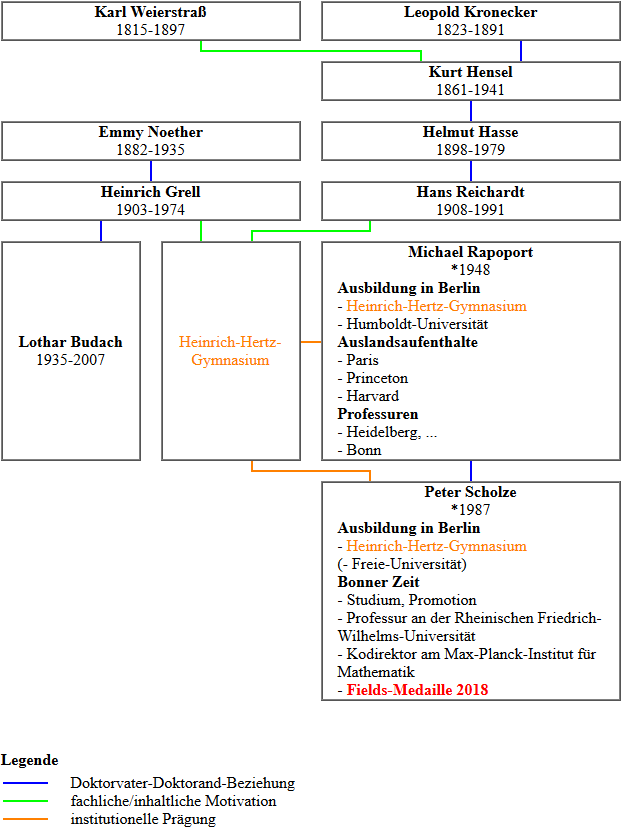
Im nachstehenden Diagramm werden die Personen und ihre Beziehungen untereinander (hauptsächlich)
aus dem berliner Umfeld ausgewiesen, die in den nachfolgenden Abschnitten eine Rolle spielen.
Die Direktoren des Max-Planck-Instituts für Mathematik (MPIM) sind hierbei absichtlich nicht
berücksichtigt.
Kurt Hensel
Kurt Hensel entstammt einer berühmten Familien-Dynastie.
Fanny Hensel (1805-1847) – getauft
Mendelssohn Bartholdy – war seine Großmutter väterlicherseits.
Zu seinem direkten Vorfahren gehört auch der Philosoph
Moses Mendelssohn (1729-1786).
Der bekannte Komponist
Felix
Mendelssohn Bartholdy (1809-1847) war Großonkel des Mathematikers Kurt Hensel.
Kurze Biografie
K. Hensel wurde in Königsberg geboren. Bis zum neunten Lebensjahr erhielt er Hausunterricht
von seinen Eltern. Dann siedelte die Familie nach Berlin über. Dort wurde sein Vater Direktor
der Deutschen Baugesellschaft. Hensel erhielt nun eine ausgezeichnete Mathematik/Physik-Ausbildung
an der Döbbelinschen Privatschule, dem späteren
Friedrich-Wilhelms-Gymnasium.
Sein Studium begann er in Bonn bei
Rudolf Lipschitz.
Er wechselte zu seinem dritten Studienjahr nach Berlin, wo er Vorlesungen bei
Karl Weierstraß und
Leopold Kronecker hörte.
Hensel fühlte sich zur Zahlentheorie hingezogen. Folgerichtig schrieb er seine Dissertation bei
Kronecker. Sie trug den Titel „Arithmetische Untersuchungen über Discriminanten und
ihre außerwesentlichen Teiler“. 1884 verteidigte er sie erfolgreich.
1886 begann Hensel an seiner Habilitation zu arbeiten – wieder bei Kronecker.
Dazwischen absolvierte er ein Freiwilligenjahr bei der Armee in Freiburg.
Dann arbeitete Hensel zunächst als Privatdozent an der Berliner Universität,
und im Jahre 1891 wurde er zum außerordentlicher Professor befördert.
Gut zehn Jahre später folgte er dem Ruf auf ein Ordinariat der
Universität Marburg (Antritt 1902). Dort blieb er bis zur Pensionierung (1930) und
darüber hinaus bis zu seinem Lebensende. Im Jahr 1917 war Hensel Vorsitzender der
Deutschen Mathematiker-Vereinigung.
Persönlich-Familiäres
Schon vor der Promotion hatte Hensel sich heimlich mit Gertrud Hahn verlobt.
Danach erst wurde dies öffentlich bekannt gegeben und ein halbes Jahr später geheiratet.
Die Ehe hielt bis an's Lebensende. Aus ihr gingen vier Töchter und ein Sohn hervor.
Selbst, wenn bereits alle Enkel von Moses Mendelssohn zum Protestantismus konvertiert waren,
unterlagen Kurt Hensel und seine Familie den ab 1933 ständig zunehmenden Repressionen gegen
die vom Regime als Juden klassifizierten Personen. Zwar griff das Gesetz zur Wiederherstellung
des Berufsbeamtentums bei ihm als bereits emeritierten Altbeamten gar nicht,
und es ist auch nicht klar, ob er von der Streichung seiner Mitgliedschaft in der
Leopoldina Kenntnis erhielt.
Hensels letzten Jahre waren dennoch von einigen diesbezüglichen Sorgen geprägt.
Am 1. Juni 1941 verstarb er in Marburg an einem Herzinfarkt.
Wissenschaftliche Leistung
Hensels wirkmächtigster Beitrag zur Mathematik war seine Erfindung der
p-adischen Zahlen. Ohne diese hätte es die
Fields-Medaille für Peter Scholze
2018 so nicht gegeben (vielleicht für eine andere Leistung, bei seinem Talent).
Hensel verband Ideen seines akademischen Lehrers Kronecker mit denen von Weierstraß.
Hensel erkundete offenbar die Möglichkeit, die Ergebnisse der Funktionentheorie auf Zahlen zu
übertragen: Um offene Probleme in der Teilbarkeitslehre ganzer Zahlen zu lösen,
betrachtete er Reihenentwicklungen
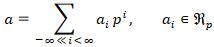
(1)
rationaler Zahlen a nach einer fixierten Primzahl p1).
Dabei ist ℜp ein fixiertes vollständiges Restsystem modulo p.
Der Einfachheit halber verwendete er das kleinste natürliche: {0, 1, 2, …, p–1}.
Hensel lässt nun in (1) alle Reihen zu, d. h. mit beliebigen Koeffizientenfolgen aus
ℜp. Sie werden p-adische Reihen genannt, und deren Gesamtheit wird
mit ℚp bezeichnet. Hensel stellte fest, dass die vier Grundrechenarten
(außer der Division durch 0) ausführbar sind. Damit ist ℚp
ein Körper, der im weiteren Körper der p-adischen Zahlen genannt wird.
Der Unterring ℤp aller Taylor-Reihen der Gestalt (1) wird
Ring der ganzen p-adischen Zahlen genannt.
Analog zur Konstruktion der reellen Zahlen mit Hilfe rationaler
Cauchy-Folgen kann
ℚp als Komplettierung von ℚ bzgl. einer p-adischen Metrik
interpretiert werden. Dies ist in Analogie zur Funktionentheorie zu den
Laurent-Reihen-Entwicklungen für
komplexe Funktionen f, die höchstens in z0 einen Pol besitzen
aber sonst in einer ε-Umgebung holomorph sind, mit der Darstellung
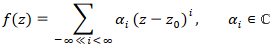
(2)
zu sehen.
(z–z0) steht hier in Analogie zu p in (1) als ein Primelement2).
Henselsches Lemma Ist das Reduktionspolynom modulo p eines normierten Polynoms
F(X) ∈ ℤp[X] teilerfremd zerlegbar in zwei normierte
Faktoren positiven Grades g(X), h(X) ∈ ℱp[X], so ist
auch F selbst in zwei normierte Faktoren G(X), H(X) ∈ ℤp(X)
zerlegbar, wobei g(X) = G(X) mod p und h(X) = H(X) mod p.
Dieses Lemma wird noch heute in den Anfangskursen der Zahlentheorie in etwas allgemeinerer Form gelehrt.
Man kann damit die Existenz einer p-adisch ganzzahligen Nullstelle eines Polynoms
F(X) ∈ ℤp[X] prüfen, indem man in der Primzerlegung
des Restklassen-Polynoms f(X) ∈ ℱp[X] über dem
Restklassenkörper ℱp := ℤ/pℤ ≅ ℤp/pℤp
einen linearen Zerlegungsfaktor g(X) entdeckt.
Allgemeine Akzeptanz in der Mathematik erhielten die p-adischen Zahlen allerdings erst,
als es Hensels Doktorschüler
Helmut Hasse in seiner Dissertation 1921 gelang,
das von Hensel als Leitlinie „erahnte“ Lokal-Global-Prinzip für
quadratische Formen über den rationalen Zahlen zu beweisen.
Meine Berührungspunkte
Diese habe ich nur aus zweiter Hand von meinem Zahlentheorie-Lehrer an der Humboldt-Universität,
Hans Reichardt. Er hörte noch Vorlesungen bei Hensel in Marburg. Dessen Vorlesungen waren unterhaltsam
mit Anekdoten von anderen Mathematikern gewürzt. Einmal fragte ihn ein Student, ob sich die Geschichten
wirklich so zugetragen haben wie er es darlegte. Hensel antwortete: „Ich erzähle die Dinge immer so,
wie sie sich eigentlich hätten zutragen müssen und nicht wie sie sich zufällig ereigneten.“
Reichardt teilte uns auch mit, dass Hensel mit seinen unendlichen Reihenentwicklungen rationaler Zahlen nach
aufsteigenden Primzahlpotenzen als ziemlich schrullig angesehen wurde. Mich selbst regte das an, mir
selbst einmal Hensels Zahlentheorie-Lehrbuch aus dem Jahre 1913 zu Gemüte zu ziehen.
Das tat ich als Student nach dem dritten Studienjahr in den Sommerferien an Spree- und Dahme-Strand
in Berlin. Mit Vergnügen konnte ich seinem klaren Aufbau bis hin zu den p-adischen Zahlen folgen.
Helmut Hasse
Kurze Biografie
H. Hasse wurde in Kassel geboren. Die Schule beendete er im Jahre 1915 mit einem Notabitur.
Er besuchte ab 1918 die Göttinger Universität. Er hörte Vorlesungen bei
Edmund Landau,
David Hilbert,
Emmy Noether und
Erich Hecke.
Sein Studium komplettierte er ab 1920 in Marburg unter starkem Einfluss von K. Hensel.
Mit großem Interesse arbeitete Hasse sich in die Theorie der p-adischen
Zahlen ein. Seine Dissertation „Über die Darstellbarkeit von Zahlen durch
quadratische Formen im Körper der rationalen Zahlen“ widmete er diesem Thema.
In seiner Habilitationsschrift „Über die Äquivalenz quadratischer Formen
im Körper der rationalen Zahlen“ setzte er erfolgreich die Anwendung der
p-adischen Zahlen fort.
Im Wintersemester 1922/23 wurde er Privatdozent an der Kieler Universität.
Es war nicht weit bis nach Hamburg. So nahm Hasse dort fruchtbare Kontakte zu
Emil Artin,
Alexander Markowitsch
Ostrowski,
Hans Petersson und
Otto Schreier auf.
Im Jahre 1925 folgte er dem Ruf einer Professur nach Halle.
Nach der Emeritierung seines Hauptlehrers Kurt Hensel im Jahre 1930 trat Hasse dessen
Nachfolge in Marburg an.
Vier Jahre später wurde er zum Direktor des Mathematischen Instituts in Göttingen berufen.
Viele wissenschaftliche Stellen in Deutschland wurden frei durch die judenfeindliche Ausdünnung
an den Instituten durch die Nazis. Während der Kriegsjahre leitete Hasse ein Forschungsinstitut
in Berlin, an dem man sich kriegsbedingt mit ballistischen Problemen beschäftigte.
Nach dem Krieg konnte er die Vorlesungstätigkeit aufgrund seiner (Mitläufer-)NSDAP-Vergangenheit
und einer britischen Besatzungsentscheidung nicht gleich wieder aufnehmen.
1946 ging er in den sowjetischen Sektor Berlins und setzte dort an der neu gegründeten
Deutschen Akademie der Wissenschaften in Berlin-Adlershof seine zahlentheoretische Forschungsarbeit fort.
Im Jahre 1949 nahm er an der Humboldt-Universität zu Berlin seine Lehrtätigkeit wieder auf.
1950 folgte er dem Ruf nach Hamburg, wo er bis zu seinem Lebensende blieb.
Er unterhielt weiterhin bis zum Jahr seiner Emeritierung, 1966, freundschaftliche Beziehungen zur Ost-Berliner
Akademie der Wissenschaften.
Nach seiner Emeritierung hielt er noch zahlreiche Vorträge im Ausland, z. B.
an der Universität von Hawaii. Helmut Hasse verstarb im Jahre 1979 in Hamburg.
Wissenschaftliche Leistung
Das folgende Resultat ist bekannt als
Satz von Hasse (Dissertation 1921): Sei
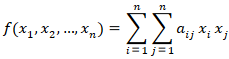
(3)
eine quadratische Form mit Koeffizienten aij in einem Zahlkörper K.
Dann folgt aus der Existenz von nichttrivialen reelle Nullstellen und in allen p-adischen
Vervollständigungen von K bereits die Existenz einer nichttrivialen Nullstelle in
demselben Zahlkörper K.
Bemerkung: Ist K = ℚ der Körper der rationalen Zahlen,
so spricht man vom Satz von Hasse-Minkowski.
Für ℚ ist auch „lokal“ (d. h. mit Hilfe aller p-adischer und reeller
Metriken) nachprüfbar, ob zwei quadratische Formen über ℚ äquivalent sind
(Habilitation).
Man sagt, dass das Hasse-Prinzip oder Lokal-Global-Prinzip in den beiden obigen
Fällen gültig ist.
Angeregt von Hilbert schrieb Hasse seinen „Klassenkörperbericht“,
der sich auf frühere Resultate von Kronecker,
Heinrich Weber und Hilbert stützt und diese weiter ausbaut.
Sei E eine elliptische Kurve über ℚ mit Konduktor N und ζ(s) die
Riemannsche Zeta-Funktion.
Die Hasse-Weil Zeta-Funktion von E hat die Gestalt
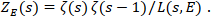
(4)
Dabei ist
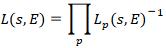
die L-Funktion von E/ℚ, mit lokalen Faktoren
- Lp(s) = 1 , wenn p2 die Zahl N teilt,
- Lp(s) = 1–ap p-s , wenn zwar p aber nicht p2 die Zahl N teilt und
- Lp(s) = 1–ap p-s+p1–2s , wenn auch p nicht die Zahl N teilt
ap = p+1, falls E gute Reduktion in p hat,
anderenfalls ap = ±1 je nachdem ob E zerfallende oder
nicht-zerfallende multiplikative Reduktion in p besitzt.
Die Hasse-Weil-Vermutung behauptet, dass die Hasse-Weil-Zeta-Funktion zu einer
meromorphen Funktion in die gesamte s-Ebene fortgesetzt werden kann und dass sie einer
Funktionalgleichung genügt. Für elliptische Kurven über ℚ folgt die Vermutung aus dem
Modul-Theorem. Im semistabilen Fall wurde die Vermutung von
André Weil bewiesen in Zusammenhang
mit dem Beweis des Fermatschen Satzes.
Erst im Jahre 2001 gelang der Beweis für alle ℚ-definierten elliptischen Kurven durch
Christophe Breuil,
Brian Conrad,
Fred Diamond und
Richard Taylor.
Das Modul-Theorem ist ein Spezialfall und wichtiger Ausgangspunkt für das umfangreiche
Langlands-Programm.
Meine Berührungspunkte
Im Rahmen des Zahlentheorie-Seminars 1964/65 wurden die Teilnehmer vom Leiter H. Reichardt
in Adlershof, Institut Mathematik und Mechanik der ehemaligen
Deutschen Akademie der Wissenschaften, Herrn Prof. Hasse vorgestellt.
Im Seminar behandelten wir das Zahlentheorie-Lehrbuch von H. Reichardts
„Hochverehrtenm Lehrer“ Hasse (laut Buchwidmung).
Ich entdeckte eine Unkorrektheit im Buch bei der Vorbereitung auf meinen Vortrag.
Prof. Reichardt regte an, dies zusammen mit einer Berichtigung, seinem Doktor-Vater nach
Hamburg zu schreiben, was ich auch tat. So kam ich als Student zu meiner ersten kleinen Publikation,
betitelt: „Eine Bemerkung zur Zahlentheorie von Hasse“. Die legte ich dazu –
und erhielt eine nette Antwortskarte aus Ahrensburg (bei Hamburg). Reichardt war wohl auch stolz,
dass die Berichtigung aus seiner Schule kam, und Hasse wusste es zu würdigen.
Hans Reichardt
Kurze Biografie
Hans Reichardt wurde in Altenburg (Thüringen) als Sohn eines Arztes geboren.
Er besuchte das Humanistische Gymnasium in Altenburg und studierte ab 1926 an den Universitäten
von Jena, Königsberg, Berlin, Hamburg und Marburg. In Berlin (ab 1928) hörte er bei
Issai Schur die Vorlesung
Algebraische Zahlentheorie. In Hamburg besuchte Reichardt die Lehrveranstaltungen von
Erich Hecke und Emil Artin. An der Universität Marburg interessierte er sich neben Mathematik auch
für Physik und Philosophie. Er promovierte dort bei H. Hasse mit der Doktorarbeit
„Arithmetische Theorie der kubischen Körper als Radikalkörper“.
Im Jahre 1934 legte er sein Lehramtsexamen ab und wurde dann Assistent an der
Universität Frankfurt bei
Carl Ludwig Siegel und 1935 in Jena bei
Friedrich Karl Schmidt.
1937 ging er an die Universität Leipzig zu
Bartel Leendert van der Waerden.
Dort habilitierte Reichardt sich 1939 mit der Arbeit „Über die diophantische Gleichung
ax + bx2y2 + cy = ez2“.
Im Jahre 1940 konnte er daraufhin dort eine Dozentenstelle besetzen. Im Krieg war er ab 1943 bei
Telefunken in Berlin beschäftigt.
Nach dem Krieg wurde er 1946 in die Sowjetunion abkommandiert. Dort arbeitete er an
Problemen der Raketentechnik auf der Insel Gorodomlja (heute Siedlung Solnetschny) im
Seligersee (Wolga-Quellgebiet). 1952 kehrte er zurück nach Berlin und erhielt eine
Professoren-Stelle an der Humboldt-Universität, wo er 1955 das Amt des Direktors des
1. Mathematischen Instituts übernahm. Ab 1959 war er Direktor des
Instituts für reine Mathematik der Deutschen Akademie der Wissenschaften zu Berlin,
wo er die Forschungsgruppe Zahlentheorie leitete. Im Jahre 1973 wurde er
emeritiert.
Wissenschaftliche und organisatorische Leistungen
H. Reichardt zeigte 1942, dass das Hasse-Prinzip nicht allgemein für
diophantische Gleichungen
gültig sein kann. Bei der Untersuchung der Arithmetik elliptischen Kurven entdeckte er eine,
die gar keinen rationalen Punkt besitzt, deren Gleichung jedoch für jede Primzahl
p eine p-adische Lösung besitzt (und auch eine reelle).
Zuvor, in den 1930er Jahren, arbeitete er über inverse Probleme der
Galoistheorie.
Er zeigte die Lösbarkeit im Fall einer p-Gruppe mit einer ungeraden
Primzahl p. Seine Arbeiten zu diesem Thema wurden unter anderem in den 1950er Jahren in
Russland von
Dmitri Konstantinowitsch
Faddejew und
Igor Shafarevich
fortgesetzt und in den 1970er Jahren in Deutschland von
Jürgen Neukirch.
Nach dem Krieg wandte er sich verstärkt der Differentialgeometrie zu. Er baute dazu eine
schlagkräftige Forschungsgruppe an der Humboldt-Universität auf, aus der
Rolf Sulanke und
Thomas Friedrich
hervorgingen. Aus der Forschungsgruppe Zahlentheorie ging
Helmut Koch hervor.
Mit der 3. Hochschulreform in der DDR wurden die Institute in „Sektionen“ umgewandelt.
Die Zahlentheorie wurde zur Akademie der Wissenschaften verlagert. Sie war dort sehr erfolgreich.
Reichardt und Koch gelang es eine enge Zusammenarbeit mit der weltweit einflussreichen
Shafarevich-Gruppe (Algebraische Geometrie und Zahlentheorie) des
Steklov-Instituts der
Akademie der
Wissenschaften der UdSSR herzustellen, wovon wir alle stark profitierten.
Ab den 1950er Jahren widmete sich Reichardt des öfteren der Mathematikgeschichte,
insbesondere zu
Carl Friedrich Gauß,
über den er 1974 auch den Artikel in der
Encyclopedia Britannica schrieb.
Unvergessen ist auch seine Herausgabe des Gauß-Gedenkbandes anlässlich dessen 100.
Todestages im Jahre 1955 (1957 erschienen im B. G. Teubner-Verlag).
Reichardt war auch Hauptinitiator der Mathematik-Olympiade in der DDR um 1960.
Ich erinnere mich daran, dass er in seiner Vorlesung über Lineare Algebra des Wintersemesters
1961/62 den ersten DDR-Olympiasieger als seinen Mathe-Enkel begrüßte.
Er kümmerte sich auch in besonderem Maße um uns Studenten. So nahm er an den
Übungsstunden stets teil. Er war oft müde, schloss die Augen, war aber sofort wach,
wenn jemand beim Vortrag an der Tafel einen Fehler machte.
Nach Abwicklung der DDR-Akademie Ende 1991 wurde die Koch-Gruppe vom MPIM aufgefangen
und alimentiert. Im Zeitraum von weniger als fünf Jahren gelang eine Lehrstuhl-Eingliederung
der Spitzenkräfte ins Institut für Mathematik der Humboldt-Universität zu Berlin.
Meine Berührungspunkte
In meinen ersten drei Studienjahren (1961-1964) war er für mich der zentrale
Mathematik-Lehrer an der Humboldt-Universität. Ich hörte bei ihm Lineare Algebra,
Algebra und Zahlentheorie mit Übungen und Seminar-Vorträgen. Anfang des dritten
Studienjahres wurden die drei erfolgreichsten Studenten der zwei Seminargruppen
unseres Jahrgangs Herrn Prof. Reichardt mit dem Anliegen vorgestellt, uns eine Sonderförderung
zuteil werden zu lassen. Wir drei Studenten dachten an ein Sonderprogramm in Richtung Algebra.
Reichardt hielt eine solche Spezialisierung für verfrüht. Wir sollten besser eine breite
Grundlage anstreben. Das taten wir dann auch und profitierten später davon.
Im 3. und 4. Studienjahr nahm ich an Vorlesung und Seminar zur Zahlentheorie teil.
H. Koch beteiligte sich an der Organisation. Es kam zu einem kleinen Streit als ich über eine
Stelle des Zahlentheorie-Buches von H. Hasse vortrug. Wie die Geschichte weiterging, wurde bereits
im Abschnitt zu Helmut Hasse/Meine Berührungspunkte dargelegt.
Ich erhielt noch in meinem 8. Semester ein Angebot von Prof. Reichardt für ein Thema einer
Diplomarbeit, das an seine eigene Doktorarbeit anknüpfte.
Es zog mich aber inzwischen schon zur Algebraischen Geometrie, die gerade von
Heinrich Grell und
Lothar Budach etabliert wurde,
siehe unten, Section 6.
Professor Reichardt und ich sollten uns aber wiedersehen. Ich erhielt 1973/74 ein Zusatzstudium
in Leningrad (heute St. Petersburg). Dort wurde ich an der Universität vom namhaften Zahlentheoretiker
Zenon Ivanovich Borevich
an das Steklov-Institut der Akademie verwiesen, und dort an den Weltklasse-Mathematiker
Boris Borissovich Venkov.
Hier arbeitete ich mich in eine Moskauer Dissertation der Vinberg-Schule ein.
Ich war fasziniert, weil Zahlentheorie, Algebraische Geometrie und Differentialgeometrie
in wunderbarer und moderner Form zusammenflossen. In einer Aufholjagd vertiefte ich mich in
die Zusammenhänge, und entwickelte die Moskauer Arbeit weiter.
Nach einem Vortrag am Banach-Zentrum in Warschau wurde der DDR-Akademie vermeldet.
„Es ist die beste Mathematik-Arbeit in Berlin nach dem Kriege“.
Prof. Helmut Koch lud mich ein, von der Universität zur Akademie zu wechseln, was ich auch tat.
Ich reichte meine wissenschaftliche Arbeit zum Doktor der Wissenschaften3) ein und
musste drei Gutachter der verschiedenen (oben genannten) Richtungen organisieren.
Es waren Prof. Helmut Koch, Prof.
Herbert Kurke und
Prof. Rolf Sulanke. Den Vorsitz bei der Verteidigung übernahm Prof. Hans Reichardt.
Bei einem Besuch des damaligen Direktors des MPIM
Friedrich Hirzebruch ermunterte
mich Reichardt, an ihm dranzubleiben, was ich auch tat. Später, nach Reichardts Emeritierung
schenkte mir dieser die Gesamtausgabe von Heckes Werken – in weiser Voraussicht,
denn ich habe sie wirklich gebraucht, bis heute.
Emmy Noether
Kurze Biografie
Emmy Noether ist wohl unbestritten die berühmteste Mathematikerin aller Zeiten.
Zur Berliner Galerie gehört sie allerdings nicht. Nur ihren Doktoranden Heinrich Grell
hatte es nach dem zweiten Weltkrieg in die Hauptstadt verschlagen. Deshalb wird hier an ihre
Persönlichkeit als eine Vorläuferin einer der Berliner Spuren im 20. Jahrhunderts erinnert.
Sie wurde im Jahre 1882 in Erlangen geboren und entstammte einer gutsituierten jüdischen Familie.
Heute erinnert eine
Tafel in der Erlanger Hauptstraße an ihr Geburtshaus.
Ihr Vater
Max Noether hatte einen Lehrstuhl
für Mathematik an der Universität Erlangen inne.
1903 holte sie in Nürnberg die externe Abiturprüfung am
Königlichen Realgymnasium (dem heutigen
Willstätter-Gymnasium) nach.
1903 wurden Frauen erstmals an bayerischen Universitäten zum Studium zugelassen,
was auch Emmy Noether die Immatrikulation an der Universität Erlangen ermöglichte.
Dort promovierte sie 1907 in Mathematik bei
Paul Gordan.
Im Jahre 1909 wurde sie von
Felix Klein und David Hilbert an die
Georg-August-Universität nach Göttingen gerufen, da sie auf dem Forschungsgebiet der
Differentialinvarianten mittlerweile eine bekannte Größe war.
Göttingen galt zu dieser Zeit als das weltweit führende mathematische Zentrum.
Durch Klein und Hilbert ermutigt, stellte Noether am 20. Juli 1915 einen Antrag auf Habilitation in
Göttingen. Der Antragstellung folgten intensive kontroverse Diskussionen in der Fakultät,
bei denen sich viele Angehörige grundsätzlich gegen eine Habilitation von Frauen aussprachen.
Letztlich konnten sich aber Hilbert und Klein durchsetzen. Berühmt wurde die in diesem Zusammenhang
gefallene Äußerung Hilberts: „Eine Fakultät ist doch keine Badeanstalt“.
Da die Habilitation von Frauen an preußischen Universitäten durch einen Erlass vom
29. Mai 1908 untersagt war, stellte die mathematisch-naturwissenschaftliche Abteilung der
philosophischen Fakultät der Universität zu Göttingen am 26. November 1915 einen
offiziellen Antrag an den preußischen Minister. Eine abschlägige Antwort kam im Jahre 1917
zurück. Emmy Noether blieb daraufhin nichts anderes übrig, als ihre Vorlesungen unter dem
Namen von Hilbert anzukündigen, als dessen Assistentin sie fungierte. Nach dem Weltkrieg konnte
sich Emmy Noether 1919 als erste Frau in Deutschland in Mathematik habilitieren.
Sie war außerdem die erste Frau in Deutschland, die eine (nichtbeamtete) Professur erhielt.
Erst 1922 erhielt sie eine außerordentliche Professur und erst 1923 ihren ersten bezahlten
Lehrauftrag.
Im Studienjahr 1928/29 übernahm sie eine Gastprofessur in Moskau und 1930 in Frankfurt am Main.
1933 wurde Emmy Noether durch das sogenannte Gesetz zur Wiederherstellung des Berufsbeamtentums
vom Naziregime ihre Lehrerlaubnis entzogen.
Ende 1933 erhielt sie eine Gastprofessur am
Womens College Bryn Mawr in Pennsylvania.
Ab 1934 hielt Emmy Noether auch Vorlesungen am renommierten
Institute for Advanced Study.
Dort wurde sie stark von
Oscar Zariski beeinflusst.
Emmy Noether verstarb am 14. April 1935 an den Komplikationen einer Unterleibsoperation,
die wegen eines Tumors notwendig geworden war.
Heinrich Grell
Kurze Biografie
H. Grell wurde in Lüdenscheid (NRW) als Sohn eines Metzgermeisters geboren.
Das Abitur legte er 1922 in seiner Vaterstadt ab. Danach studierte er Mathematik, Physik und
Astronomie an der Universität Göttingen und promovierte im Jahre 1926 bei Emmy Noether
mit der Dissertation „Beziehungen zwischen den Idealen verschiedener Ringe“.
Mit Hilfe eines Stipendiats der
Notgemeinschaft
Deutsche Wissenschaft betätigte er sich 1927/28 als Hilfsassistent in Göttingen.
Danach arbeitete er bis 1930 als Assistent an der Universität Jena, schrieb dort seine
Habilitations-Arbeit „Verzweigungstheorie in beliebigen Ordnungen algebraischer Zahl- und
Funktionenkörper“ und war hernach kurzzeitig Dozent.
Er musste sich dann mathematisch umorientieren, habilitierte sich 1934 erneut in Halle und
wurde nun Dozent für Analysis und Analytische Geometrie.
1935 wurde H. Grell wegen Verstoßes gegen §175 des Strafgesetzbuchs (homosexuelle Handlungen)
inhaftiert und verlor seine Lehrbefugnis. Der damalige Vorwurf erscheint mir an den Haaren herbeigezogen,
da ich ihn als verheirateten Ehemann kannte. Von 1935 bis 1939 war er arbeitslos und hielt sich mit
Gelegenheitstätigkeiten über Wasser.
Der Krieg holte ihn in die Messerschmitt-Flugzeugwerke. Dort war er bis 1944 Gruppenleiter in der
Entwicklungsabteilung. Im letzten Kriegsjahr wurde er in den Reichsforschungsrat mit Sitz in Erlangen
berufen. Nach Kriegsende nahm er seine Assistententätigkeit wieder auf, nacheinander an den
Universitäten Erlangen und Bamberg. 1948 nahm er einen Ruf an die Humboldt-Universität
zu Berlin (HU) an, der er bis zu seiner Emeritierung im Jahr 1968 angehörte. Dazwischen siedelte
er nach dem 17. Juni 1953 von Westberlin in den Ostteil der Stadt über, da es am Grenzübergang
auf seinem Weg vom Wohnsitz zur HU zu Behinderungen kam, wie er einmal erzählte.
Von 1959 bis 1962 übte H. Grell die Tätigkeit des geschäftsführenden Direktors am
Institut für Reine Mathematik der ehemaligen Deutschen Akademie der Wissenschaften in
Berlin-Adlershof aus. Er stieg 1964 zum stellvertretenden Generalsekretär der gesamten Akademie auf
und blieb acht Jahre in dieser Funktion.
Heinrich Grell starb im Jahr 1974 in Berlin.
Meine Berührungspunkte
Ab dem 4. Studienjahr nahm ich am gut besuchten Seminar Algebraische Geometrie teil,
das von H. Grell und vom jungen talentierten Akademie-Forscher Dr. Lothar Budach geleitet
wurde.4)
Parallel dazu besuchte ich auch die Grellsche Vorlesung Satz von Riemann-Roch (mit algebraischer
Beweisführung). Beeindruckend waren für mich die Grundlagen von
Richard Dedekind und Emmy Noether,
auf die zurückgegriffen wurde, um dann zu moderner Darstellung vorzustoßen.
Es war seine letzte Vorlesung.
Ende des Studienjahres bat ich Grell um ein Thema für meine Diplomarbeit. Ich suchte mir das Thema
„Idealtheorie in μ-noetherschen Ringen“ aus. Darüber hinaus bat ich um einen
Termin in der Akademie, um über das Diplomstudium hinaus weiter algebraisch-geometrisch als
Assistent beschäftigt zu werden. Schon die schwere Eingangstür zum Zimmer mit der Aufschrift
„Stellvertretender Generalsekretär“ beeindruckte mich sehr.
Es befand sich im Akademiegebäude gegenüber dem Gendarmenmarkt (zu DDR-Zeit
„Platz der Akademie“). Im Gespräch machte Grell darauf aufmerksam,
dass ein breites Grundwissen nötig ist und ich auf jeden Fall auch einen guten Abschluss im
Nebenfach „Theoretische Physik“ bräuchte. Außerdem legte er mir nahe, den zweiten
Bande der „Kommutativen Algebra“ von Oscar Zariski und
Pierre Samuel durchzuarbeiten.
Die beiden Bände hatte ich mir schon zuvor auf russisch zugelegt, den ersten schon früher
verschlungen. Man konnte sie preisgünstig im Haus des Sozialistischen Buches
in der Nähe des Neptunbrunnens kaufen. Zielstrebig lernte ich nun und hielt ein Jahr später
das Diplomzeugnis mit der Gesamtnote „ausgezeichnet“ in den Händen.
Pünktlich im September 1966 trat ich dann an der Humboldt-Universität, Sektion Mathematik,
die planmäßige Aspirantur3) an. „Idealtheorie in abelschen Kategorien“
war das Thema meiner Dissertation, für die mir drei Jahre zur Anfertigung eingeräumt
wurden, die ich auch einhielt. Das Grell-Budach-Seminar lief weiter, wobei das Niveau mit der Orientierung
auf das gemeinsame Studium internationaler Spitzenarbeiten auf dem Gebiet der algebraischen Geometrie
(Grothendieck, Deligne, Shafarevich) deutlich angehoben wurde. Ich war Grells
letzter Doktorand. Die Hauptergebnisse meiner Dissertation flossen in die Monographie
„Localisations and Grothendieck Categories“ ein, die L. Budach zusammen mit mir verfasste.
Wissenschaftlich-organisatorische Leistungen
Aus der Zeit nach dem 2. Weltkrieg ist mir keine wissenschaftliche Arbeit von Heinrich Grell bekannt.
Er war hauptsächlich in der Lehre und der Organisation des Wiederaufbaus einer
starken Mathematik in Deutschland beschäftigt. Es gelang ihm, eine starke Schule der algebraischen
Geometrie in der DDR aufzubauen. Zusammen mit dem Professor H. Reichardt initiierte er in den
1960ern die Einrichtung einer Spezialschule mit mathematisch-naturwissenschaftlicher Ausrichtung,
die erste in Deutschland. Dazu wurde das Heinrich-Hertz-Gymnasium in Berlin-Adlershof auserkoren,
das heute noch existiert (nach zweimaligem Umzug innerhalb Berlins). Inzwischen haben wir einen
Fieldsmedaillen-Preisträger, der durch diese Schule ging (P. Scholze, 2018).
Es noch angemerkt, dass auch bereits die Doktormutter E. Noether und der Doktorvater H. Hasse von
H. Grell bzw. H. Reichardt um 1930 zusammenarbeiteten. Ein wissenschaftlicher Briefwechsel
(1925-1935) zwischen beiden zu tiefen algebraischen Problemen ist erhalten und im Internet
einzusehen.5)
Die Budachsche Jugend-Forschungsgruppe
Während meines ersten Jahrs als Doktorand wurde das Seminar Algebraische Geometrie
umgewandelt in eine vertikale Lern- und Forschungsgruppe. Die besten Studenten über sechs
Studienjahre (zum 6. wurde ich auch gezählt), die sich für algebraische Geometrie interessierten,
wurden zusammengefasst. Für ein gemeinsames Forschungsprojekt konnten die Studenten
Marko Roczen und
Gerhard Pfister
sofort gewonnen werden.
Mir wurde die Aufgabe zuteil, die beiden heranzuführen. Unsere gemeinsame Arbeit
„Primärzerlegung in abelschen Kategorien“ brachte uns zur
Messe der Meister von morgen (MMM)
nach Leipzig. Ich erinnere mich, dass Regierungschef Willy Stoph die Stände um uns herum besuchte
und Gisela Mai zum MMM-Ereignis einige Lieder in einer Abendvorstellung sang.
G. Pfister wurde in den 1970ern an der HU zum Professor berufen, nach der Wende nach Kaiserslautern.
Des weiteren stießen drei sehr begabte Absolventen des Heinrich-Hertz-Gymnasiums zu uns.
Sie hatten schon die Mathe-Kenntnisse des Grundstudiums intus. Sie erhielten nämlich
zusätzlich zum mathematisch orientierten Schulstoff am Gymnasium durchgängig eine
Sonderförderung durch Prof. L. Budach. Er bezog sie sogleich in unsere Gruppe ein.
Bei ihrer ersten Teilnahme trug ich gerade über Étal-Topologie vor.
Es muss für sie ein Schock gewesen sein, aber sie blieben dabei, überholten uns nach und nach
und zwei von ihnen wurden später Professoren in den (noch) alten Bundesländern.
Sie gehörten bereits seit ihrer BRD-Zeit mit zur Weltspitze:
Michael Rapoport und
Thomas Zink.
Um Mittel für Herbstschulen und Teilnahme an Konferenzen zu erhalten und auch um lästige
Nebenbeschäftigungen in den jeweiligen Seminar-Jahrgängen zu vermeiden, wurde die
Budach-Gruppe in den Status einer FDJ-Gruppe
(Freie Deutsche Jugend)
erhoben. Als Polit-Thema wählten wir die „Marxistische Durchdringung der Mathematik“.
Hauptsächlich behandelten wir dabei philosophische Fragen, an die (unsere) Wissenschaft
bekanntlich nicht arm ist.
Es musste allerdings noch ein FDJ-Gruppenorganisator gefunden werden. Da ich wissenschaftlich am weitesten
fortgeschritten war (siehe obiges Gutachten von H. Grell, das ich nach der Wende in meiner Kaderakte
fand), wurde ich vorgeschlagen. Ich bemerkte, dass ich nicht Mitglied der Organisation bin.
„Das macht nichts, merkt doch keiner“ wurde mir entgegnet. Und schwupps war ich gewählt.
Na gut, ich schrieb ein Programm, das uns fachlich vorwärts in Richtung Weltniveau bringen sollte.
Politisch waren die Zeiten auch brisant (1967/68). Frühere Probleme mit der FDJ habe ich
wohlweislich verschwiegen: Meine Eltern hatten mir einst strikt verboten, in Pionierorganisation
bzw. FDJ einzutreten (auch diese Art Diktatur hat es in der DDR vereinzelt gegeben).
Ich musste damals auf Umwegen zu Abitur und Studium gelangen.
In Frankreich und Westberlin gab es große Demonstrationen. Der Fields-Preisträger
Alexander Grothendieck,
dessen bahnbrechende Arbeiten wir studierten, widmete sich mit seinem Appell „Survivre“
(Überleben) der weltweiten Abrüstung. Wir wandten uns an ihn,
wollten ihn für einen Vortrag an die Humboldt-Universität einladen.
„Ja“ schrieb er zurück, „er würde gern kommen, möchte aber dann auch
mit den Studenten öffentlich diskutieren.“
Dem folgte eine kalte Dusche von der Parteileitung der Sektion Mathematik:
„Dieser Pazifist kommt uns nicht ins Haus!“.
Ich stieß an der Universität im Vorfeld des Prager Frühlings auch auf die Meinung
einiger Studenten:
„Die beiden Systeme – Kapitalismus und Sozialismus – bewegen sich
aufeinander zu“. Diese Ansicht lief unter dem Namen „Konvergenztheorie“.
Das klang auch ein bisschen mathematisch, stärker noch bei der Abkürzung
„K-Theorie“. Denn wir befassten uns im Seminar auch mit der mathematischen
K-Theorie, mit deren Hilfe man die
Riemann-Roch-Theorie höherer Dimensionen besser verstehen konnte. Nun musste ich zum
Promotionsabschluss auch eine gesellschaftswissenschaftliche Arbeit abliefern, die von der
GeWi-Fakultät betreut wurde. Mir wurde das Thema der gesellschaftlichen Konvergenztheorie angeboten,
mit dem Ziel, sie zu widerlegen.
Ich bat dafür um Literaturhilfe und erhielt die Möglichkeit bis zur Fertigstellung meiner Arbeit
(ca. drei Monate), den Giftraum der Staatsbibliothek Unter den Linden zu inspizieren.
Gleich fiel mir hinter der Tür die Sammlung von Nazi-Zeitungen ins Auge:
Der Völkische Beobachter und Der Stürmer.
Die konnten mir natürlich nicht weiter helfen. Ich entdeckte auch den SPIEGEL,
den ich gleich schätzen lernte. Des weiteren standen u. a. folgende Autoren auf dem DDR-Index:
Ota Sik („Der Rote Erhard aus Prag“),
Karl Jaspers,
Zbigeniev Brzeziński,
Kenneth Galbraith,
Jan Tinbergen (Nobelpreisträger
in Ökonomie). Sie (und viele andere) waren mir nun zugänglich. Mir gelang es damit,
überzeugend gegen die Konvergenzthese zu argumentieren. Es war ein Konstrukt des Kalten Krieges
aus westlicher Richtung. Die weitere Entwicklug bis zum Zusammenbruch der Sowjetunion sollte mir Recht
geben.6) Jedenfalls setzte ich das Thema „K-Theorie“
bei einer unserer Herbstschulen auf die Tagesordnung. Wir hatten einen zweistündigen regen
Meinungsaustausch.
Nachdem ich 1969 Assistent an der Mathe-Sektion wurde, hatte ich plötzlich nur noch wenig Zeit.
Neben Seminargruppenbetreuunf frisch immatrikulierter Studenten und der Betreuung zweier Übungsgruppen
wurde mir auch die Leitung eines Forschungsseminars übertragen, das sich mit dem Thema
„Algebraische Flächen“ nach dem gleichnamigen Buch – frische Übersetzung
einer Broschüre des Steklov-Institutes Moskau, die damals unter Leitung von I. R. Shafarevich
herausgegeben wurde – beschätigte.
Das war nicht leicht zu verstehen, für meine Zukunft aber ziemlich wertvoll.
Ich wurde zum Erlernen „programmierten Unterrichts“ zu einem Lehrgang nach Leipzig delegiert.
Dies war eine ergebnisarme Schiene, auf die ich geschubst wurde, ebenso wie die Kategorientheorie.
Ich musste erst ein Jahr zum Zusatzstudium nach Leningrad kommen (1973/74) um eine Aufholjagd mit
einem neuen interessanten Thema der algebraischen Flächentheorie von internationalem Interesse zu
starten.
Michael Rapoport
Die Eltern
Seine Mutter (Ingeborg Rapoport)
wurde 1912 geboren, wuchs in Hamburg auf, studierte dort Medizin, schloss mit dem Staatsexamen 1937 ab.
Ihre Dissertation durfte sie aber wegen der damaligen antijüdischen Gestzgebung nicht
verteidigen, was sie allerdings im Jahre 2015 mit Bravour im Alter von 102 Jahren in Hamburg nachholte.
Sie reiste 1938 in die USA aus, lernte 1944 an der University of Cincinnati ihren späteren Mann
Samuel Mitja Rapoport kennen,
der aus Österreich emigriert war.
Nach der Geburt des zweiten Sohnes (Michael Rapoport) mussten sie wieder mal das Land verlassen,
um nicht wegen „unamerikanischen Verhaltens“ in der McCarthy-Ära angeklagt zu werden.
So gelangten sie über Österreich in die DDR, wo beiden eine beachtliche medizinische bzw.
biochemisch-wissenschaftliche Laufbahn gelang.
Der Sohn Michael Rapoport
Wegen der Herkunft seines Vaters besaß er die österreichische Staatsbürgerschaft und
gab diese mit Erreichen der Volljährigkeit in der DDR auch nicht auf. Er bemerkte später
einmal scherzhaft, dass er aufgrund seines Geburtslandes noch Staatspräsident der USA werden
könne. Seine Schulbildung erhielt er in der DDR. In der (mathematisch ausgerichteten)
Heinrich-Hertz-Schule in Berlin-Adlershof legte er 1967 das Abitur ab. Danach nahm er das
Mathematik-Studium an der Humboldt-Universität zu Berlin auf, mit starker Förderung in der
Budachschen Lern- und Forschungsgruppe.
Nach dem Diplom setzte er vertieft sein Studium in Paris, Princeton sowie Harvard fort.
Von den Fields-Medaillisten
Pierre Deligne (Paris) und
David Mumford (Harvard) wurde er dabei
weiter gefördert und an die Weltspitze herangeführt. Er promovierte 1976 an der Universität
Paris-Sud bei Pierre Deligne mit der Dissertation „Compactifications de l'espace de
modules de Hilbert-Blumenthal“.
Danach kehrte er nach Berlin zurück, wo er bis 1980 als Assistent an der Sektion Mathematik
arbeitete. Leider wurde M. Rapoport nicht seines hohen Wissensstandes gemäß beschäftigt.
Es fehlte die damals erwünschte politische Komponente. H. Koch wollte ihn noch –
mit Zustimmung all seiner Mitarbeiter – in die eigene Forschungsgruppe zur Akademie holen.
Aber sowohl von der Institutsleitung als auch von Rapoport selbst gab es keine Zustimmung.
Er verließ die DDR in Richtung Bundesrepublik und bekleidete von 1982 erfolgreich
Professorenstellen in Heidelberg, Bonn, Wuppertal und Köln. Seit 2003 hat er den Lehrstuhl
für Arithmetische Algebraische Geometrie an der Universität Bonn inne.
Die zahlreichen Auszeichnungen sind im
Wikipedia-Beitrag aufgelistet.
Seine Top-Leistung ist nun die
Heranführung von Peter Scholze, nach dessen Abitur am Heinrich-Hertz-Gymnasium,
zur Fields-Medaille 2018. „Ich platze vor Stolz“ war seine Reaktion kurz nach
der Verleihung. Das kann man uneingeschränkt nachempfinden.
Das Heinrich-Hertz-Gymnasium
Im Jahr 1961 wurde der damals in Adlershof befindlichen Erweiterten Oberschule (EOS) der Name des
Physikers
Heinrich Hertz verliehen.
Die Profilierung in Richtung Mathematik entstand erst allmählich
mit lebhafter Unterstützung der HU-Professoren Hans Reichardt und Heinrich Grell.
1963 wurde die erste mathematisch orientierte 9. Klasse eingerichtet.
Ab 1965 wurde die Heinrich-Hertz-Oberschule eine Schule mit mathematischem Schwerpunkt,
1969 waren dann alle Klassen der Schule mathematisch orientierte Spezialklassen.
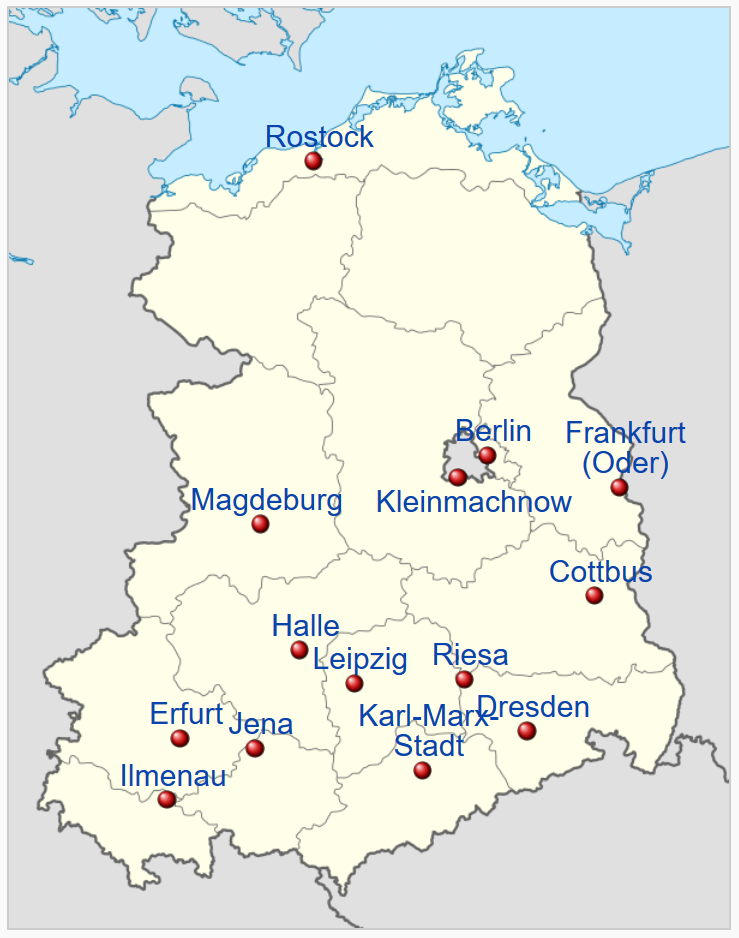
Unter mathematisch-naturwissenschaftlich interessierten Schülern wurde die Schule
berlinweit und darüber hinaus bekannt. Nach ihrem Vorbild entstanden dann in fast allen 15
Bezirken der DDR derartig ausgerichtete Spezialschulen, siehe nachstehende Landkarte.
Dies geschah wohl ähnlich wie im DDR-Sport.
Eine Zeitzeugin soll nun betreffs der Atmosphäre an dieser Schule in den 1960er Jahren zu
Worte kommen, nämlich Ingeborg Rapoport7):
„Dies ist die einzige Schule, die ich meinem Leben von ganzem Herzen gehasst habe,
obgleich sie fachlich ausgezeichnet war und den Schülern in der Tat eine hervorragend solide
Vorbereitung für Mathematik und Naturwissenschaften, aber auch für geisteswissenschaftliche
Fächer, vermittelte.
Im Gegensatz zu den Sonderklassen an der Humboldt-Universität, an denen mit großem
Feingefühl auf die politischen Fragen und Zweifel, auf eigenes Suchen nach individuellen
Antworten der Jugendlichen eingegangen wurde, herrschte an der Heinrich-Hertz-Schule zu jener Zeit
ein unerbittlich sektiererischer Geist. Die halbwüchsigen Kinder, sämtlich kleine
,Intelligenzbestien‘, hatten selbstverständlich viele Fragen politischer Art,
weltanschauliche Bauchschmerzen und natürlich ein Bedürfnis nach eigenem Urteil.
Zwischen den Buben und Mitja gab es während ihrer Pubertätszeit viele leidenschaftliche
Diskussionen, die von Mitja oft zu hart geführt wurden. ... Zu Hause spielten sich solche
Diskussionen, so schmerzhaft sie auch manchmal waren, auf einem Untergrund starker und
unerschütterlicher Liebe ab. An der Heinrich-Hertz-Schule unter ihrem Direktor
herrschte damals tiefstes Misstrauen gegenüber diesen Kindern.
Jede ihrer Fragen wurde als politische Provokation gedeutet, und ich zweifle auch nicht daran,
dass aus den ursprünglich 'unschuldigen' Fragen und Bemerkungen allmählich ein aufsässiger
Ton entstand – ein böser Circulus Vitiosus, der sich schließlich in einer solchen
Art schloß, dass sechs Kinder der Klasse als 'feindliche Elemente' die Relegierung von der Schule
drohte, darunter auch Michael. Es gab, soweit wir Eltern es übersehen konnten, nur die
Deutschlehrerin, die versuchte, ein vernünftiges Gegengewicht gegen die wahre Hexenjagdatmosphäre
an der Schule zu schaffen.
Ich will Michaels Zeit an der Heinrich-Hertz-Schule nicht ganz und gar in Grund und Boden verdammen.
Sie hatte auch einen entscheidenden positiven Faktor für seine fernere Zukunft. Ein junger
Professor der Mathematik an der Humboldt-Universität, späteres Mitglied der Akademie der
Wissenschaften, Professor Budach, interessierte sich für die begabten Kinder und bot ihnen an,
mit an seinem Forschungsthema zu arbeiten. Zunächst waren es fünf oder sechs,
die mitmachen wollten, aber schließlich blieben nur zwei8)
Michael und Thomas Zink, sein lebenslanger Freund.“
Mit den Wendeereignissen 1990 mussten sich alle DDR-Spezialschulen umorientieren.
1991 wurde der Antrag auf Errichtung eines Gymnasiums mit mathematisch-naturwissenschaftlicher
Profilierung genehmigt. Derzeit, d. h. im Jahr 2019, existiert z. B. ein Leistungskurs für mathematisch
besonders begabte Schüler, der bereits studiumsrelevanten Stoff behandelt und bei sehr guten
Leistungen den Erhalt von universitär gültigen Leistungsnachweisen einschließt.
Für alle Schüler gibt es wählbare Erweiterungskurse in Mathematik und Physik mit
Themen wie Einführung in die „Theorie gewöhnlicher Differentialgleichungen“
und „Metrischer Räume“.
Namhafte Absolventen:
- 1966: Gregor Gysi, Politiker,
- 1967: Michael Rapoport, Mathematiker,
- 1970: Klaus Altmann, Mathematiker,
- 1976: Jürgen Kuttner, Radiomoderator,
- 1983: Yuri Tschinkel, Mathematiker,
- 1985: Alexander Schmidt, Mathematiker,
- 1985: Daniel Huybrechts, Mathematiker und
- 2007: Peter Scholze, Mathematiker, Träger der Fields-Medaille.
Die Mathematik-Lehrer von P. Scholze an der HH-Schule stellten fest, dass er bei ihnen nichts
mehr lernen könne. Mein Ex-Kollege Prof. Altmann, inzwischen Inhaber des Lehrstuhls
für Algebraische Geometrie an der Berliner Freien Universität, nahm sich des jungen
Talents an und förderte ihn mit einem Spezialprogramm. Nach Absolvierung desselben
(und Abiturabschluss) meldete sich Scholze zu einer Konsultation in Bonn bei M. Rapoport.
Letzterer war beeindruckt und nahm ihn unter seine Fittiche bis zum
Fieldsmedaillen-Niveau.
Kritische Bemerkung zur Schulchronik
In der Schulchronik des Heinrich-Hertz-Gymnasiums wird
- 1967: Thomas Zink, Mathematiker
Auch sei bemerkt, dass die Hauptinitiatoren der Mathe-Profilierung in den 1960ern nicht
in der Schulchronik erwähnt werden. Im Ausland, speziell in Großbritannien,
hingegen weiß man die Erfolge zu würdigen. Im
MacTutor History of Mathematics
archive findet man zu Hans Reichardt folgenden Text der Autoren J. J. O'Connor und E. F. Robertson:
„We should mention another aspect of Reichardt's contributions, namely his work with the
Heinrich-Hertz-Gymnasium in Berlin. ... The school only received its mathematical emphasis in 1965
through the efforts of Reichardt and his colleague at the Humboldt University in Berlin,
Heinrich Grell (1903-1974)“.9)
Ein einziges Mal besuchte ich selbst das Heinrich-Hertz-Gymnasium. Darauf komme ich am Ende des
Abschnitts zu Gerd Faltings zurück.
Zum Gründungsdirektor des MPIM Friedrich Hirzebruch (1927-2012)
Hier soll nicht das Lebenswerk von
Friedrich Hirzebruch beschrieben
werden. Vielmehr präsentiere ich ein paar Episoden einer Ost-West-Odyssee, die mir eine
fachliche (und menschliche) Annäherung ermöglichten.
Sein Name fiel mir zuerst (1973 in Berlin) als Autor der russischsprachigen Monographie
„Topologitscheskije Metodi w algebraicheskoj geometrii" auf. Das Original erschien bei
Springer schon 1966. Die Übersetzung stammte von B. B. Venkov. Nun konnten wir
es in der DDR (für 5 DDR-Mark) kaufen und darin lesen.
Im September 1973 wurde ich zum einjährigen Zusatzstudium in die Sowjetunion delegiert.
Als Wunschziel hatte ich – wie fast alle Delegierten – Moskau angegeben,
wurde aber nicht erhört. Dort, an der Lomonossow-Universität, hatte man beste
Arbeitsbedingungen (mit eigenem Zimmer) und guter Betreuung. Ich wollte meine Hinreise auch
individueller gestalten, da ich an der Einschulung der Tochter Anfang September teilnehmen wollte.
Ging auch nicht, musste mit dem Delegationszug mitfahren, zunächst nach Moskau.
Dort wurden wir dann in kleineren Gruppen auf Züge zu den jeweiligen Zielorten,
die von verschiedenen Bahnhöfen abfuhren, verteilt. Ich wurde nach Leningrad (heute St. Petersburg)
befördert, dort zum Studentenheim auf der Wassiljew-Insel, Detskaja Uliza 10.
Mit zwei Russen und einem Dresdner Kollegen bezog ich ein Zimmer mit Gemeinschaftsküche,
-waschraum und -toilette (alles für den gesamten Flur).
Am nächsten Tag meldeten wir Neuangekommenen uns in der Leningrader Universität,
wo wir auf unsere Betreuer aufgeteilt werden sollten. Mit jedem wurde ein Gespräch geführt,
um dann eine geeignete Zuordnung zu treffen. Im Mathematikraum saß kein Geringerer als
Z. I. Borevich (1922-1995), dessen Buch „Zahlentheorie“, das er zusammen mit
I. R. Shafarevich verfasst hatte, unter Algebraikern sehr bekannt war.
Ich nannte ihm internationale Arbeiten, die zu Hause bereits studiert wurden, auch russische
(Manin, Shafarevich). Er sagte: „Tut mir leid, hier an der Universität können
Sie von keinem unserer Lehrstuhlinhaber etwas dazu lernen.“
Ich bin also vom Hochschulministerium der DDR (oder von hintergründigem Personenkreis)
offenbar in die „Wüste“ geschickt worden, dachte ich bei mir.
Nachdem wir noch auf DDR-Namen stießen, die wir beide kannten (aus den Forschungsgruppen von
H. Reichardt und H. Koch), meinte Borevich: „..., dass ich nicht ganz umsonst gekommen sein muss.
Nicht weit von hier, an der Fontanka, befindet sich die Leningrader Abteilung des
Steklov-Institutes für Mathematik der Akademie der Wissenschaften der UdSSR.
Dort arbeitet B. B. Venkov. Von dem können Sie garantiert noch einiges lernen.“
Aha, der übersetzer des Hirzebruch-Buches. Ich meldete mich bei ihm, und er lud mich in sein
Forschungsseminar Algebraische Geometrie und Zahlentheorie ein.
Es wurde gerade die aktuelle Arbeit des italienischen Fields-Preisträgers
Enrico Bombieri behandelt.
Nach drei Wochen merkte ich, dass ich ja dafür auch hätte zu Hause bleiben können.
Ich wollte mich an einem aktuellen russischen Forschungsprojekt direkt beteiligen, wenn ich nun schon
mal da bin. „Na gut“ meinte er, „ich habe eine Moskauer Dissertation zu begutachten,
kommen Sie mit ins Boot.“ Das wollte ich tun. Damit war ich zunächst einige Zeit mit der
Uuml;bersetzung aus dem Russischen ins Deutsche beschäftigt, schriftlich und formal.
Zum Verständnis fehlte mir eine Menge klassisches und modernes Wissen. Die Kombination von
Differentialgeometrie, Zahlentheorie, Topologie, Analysis und algebraischer Geometrie faszinierte mich sofort.
Bei uns in der DDR liefen die Richtungen in getrennten Forschungsgruppen, deren Leiter kaum
miteinander (fachlich) kommunizierten. Eine Aufholjagd musste beginnen, um alles zu verstehen und
dann weitere Flächenkonstruktionen – über die des Moskauer Doktoranden
hinaus – zu erschließen.
B. B. Venkov verwies mich nun auf Arbeiten von Hirzebruch, in die er sich selbst vertieft hatte
und Neues aus Bonn ständig im Auge behielt. Er hob hervor, dass ich wichtige Arbeiten von dort
sprachlich gut verstehen könne. „Dort liegt die Zukunft“, meinte er noch.
Vor meiner Rückkehr nach Berlin bat ich ihn, mir diesen Satz schriftlich zu geben,
um in dieser Richtung an der Humboldt-Universität weiterarbeiten zu können.
Ich legte die Venkovsche Empfehlung meiner Sektion zu Hause vor, erntete aber dort Unverständnis.
Ein Kollege klopfte mir etwas später auf die Schulter und erzählte mir von einer
Parteiversammlung, auf der besprochen wurde, dass wir keine Themen von NATO-Staaten annehmen wollen.
Ich konterte mit einer DDR-Losung, die oft auf Transparenten zu lesen war:
„Von der Sowjetunion lernen heißt siegen lernen“. Den Widerspruch musste ich wohl
selbst lösen. Und das tat ich. Im Kopf hatte ich dabei einen Beatles-Titel: „I'll follow the sun“.
Zur Aufholjagd gehörten jetzt inhaltlich auch die Hilbertschen Modulflächen,
die von Hirzebruch und einigen seiner Schüler bearbeitet wurden. Sie boten eine gute Leitlinie.
Die Flächen, die mit der Moskauer Dissertation ins Blickfeld gerieten, nannte ich
Picardsche Modulflächen, da sie aus Arbeiten von
Émile Picard hundert Jahre
früher bei Monodromie-Untersuchungen (Mehrdeutigkeiten) spezieller komplexer Funktionen
in zwei Variablen heraussprangen.
Leider musste ich die Arbeit wegen Einberufung zum halbjährigen Reservistendienst in die Armee
(NVA, Nationale Volksarmee) als Soldat Dr. Holzapfel unterbrechen. Ich las in der knappen Freizeit
weiter die Arbeiten von Hirzebruch. Immerhin wusste so eine ganze Kompanie aus berufenem Mund,
dass die Wissenschaft in Bonn ein ganzes Stück weiter war, als wir in der DDR.
Fanden alle sehr interessant. Das rief auch die Staatssicherheit auf den Plan.
Eines Tages gab es eine besondere Kontrolle meines Schrankes. Sie fischten die Hirzebruch-Arbeiten
aus einem Fach heraus. Nach einer Woche bekam ich sie vollständig zurück mit der Bemerkung,
dass sie darin nichts Politisches gefunden hätten. Ich durfte weiter lesen.
Zu Hause hatte inzwischen mein Doktorand
Jan-Michael Feustel –
Sohn der „Pittiplatsch“-Schöpfer des DDR-Fernsehens – fleißig weiter
an den Picardschen Modulflächen gearbeitet. Er hatte nach sehr guter Diplomarbeit zu diesem
Thema eine Stelle in der Forschungsgruppe von H. Koch erhalten, ohne jegliche Lehrverpflichtung.
Nach meinem Armeedienst legten wir zwei uns zusammen weiter ins Zeug. Es muss 1977 gewesen sein
als ein Besuch von Hirzebruch in Berlin zusammen mit einigen anderen BRD-Mathematikern angekündigt wurde.
An unserer Sektion wurden Betreuer eingeteilt, die die Gäste am Bahnhof Friedrichstraße
abholen und zum Hotel geleiten sollten. Die Zuordnungen waren nicht fachlich passend verteilt.
Mit einem Kollegen vereinbarte ich einen Tausch: Mich zog es zu F. Hirzebruch.
Bei der Fahrt zum Hotel kam ich sogleich mit Herrn Hirzebruch mathematisch ins Gespräch.
Ich konnte schon einige Ergebnisse vorweisen. Hirzebruch zeigte sich sofort interessiert,
fand schnell Zugang zu meinen Gedankengängen. Nach den Vorträgen der Gäste saßen
wir noch länger zusammen. Er gab mir wertvolle Ratschläge und übergab mir auch neueste
Arbeiten von seinen Doktoranden, die an Hilbertschen Modulflächen arbeiteten.
Im Laufe eines Jahres verfasste ich die ersten zwei Kapitel meiner
„Kugelquotientenflächen“ als Broschüre in den Seminarberichten,
die von der Sektion Mathematik der Humboldt-Universität herausgegeben werden. Ein Exemplar
sandte ich nach Bonn.
In einer Woche im Mai 1978 wurde das Leopoldina-Symposion Singularitäten
vom MPIM im Schloss Reinhardsbrunn in Thüringen organisiert.
Die Leopoldina
ist die älteste dauerhaft existierende naturforschende Akademie der Welt, gegründet im Jahre 1652.
Ihr Hauptsitz befindet sich seit 1878 in Halle (Saale). Als älteste naturwissenschaftlich-medizinische
Gelehrtengesellschaft im deutschen Sprachraum blieb sie weitgehend frei von staatlicher Einflussnahme
und ihrem gesamtdeutschen Charakter treu, auch in den DDR-Jahren. Es sei noch erwähnt, dass die
Akademie im Juli 2008 zur Nationalen Akademie der Wissenschaften ernannt wurde.
Mehr historische Details findet man im Wikipedia-Artikel zur Leopoldina im Abschnitt
Geschichte.
Heute kommt es mir so vor, als hätte man die jährliche Bonner Arbeitstagung des MPIM
entlang der Leopoldina-Schiene in die DDR verschoben. So etwa war die namhafte internationale
Beteiligung aus Ost und Weast. Die Finanzierung kam zweifellos aus der BRD.
Ich erinnere mich besonders an die Teilnahme des Fields-Preisträgers David Mumford (USA) sowie
an die Spezialisten für Singularitäten
Eduard Looijenga (Holland),
Henry C. Pinkham (USA) und
Egbert Brieskorn (Bonn, Meisterschüler
von Hirzebruch). Letzterer schimpfte sehr, dass allen eingeladenen Russen die Ausreise aus der
Sowjetunion in die DDR verweigert wurde. Brieskorn hätte speziell
Wladimir Igorewich Arnold
(Moskau) gern getroffen.
Auch die Unterbringung im schönen Schloss Reinhardsbrunn (bei Friedrichroda) erschien mir
irgendwie eine gesamtdeutsche Linie zu repräsentieren. Erstaunt war ich, dass in jedem
Nachtschränkchen die Bibel zu finden war. Tatsächlich diente das Schloss seit 1953
als (exquisites) Hotel des VEB Reisebüro der DDR, vor allem als Devisenbringer für Gäste
aus dem nichtsozialistischen Ausland. Es entwickelte sich dabei auch zum Kultur-und Bildungszentrum,
an dem Konzerte und Kongresse stattfanden. Zur langjährigen Geschichte (1085-2018) sei auf diesen
Wikipedia-Artikel verwiesen.
Im Jahr 2018 wurde es (wieder einmal) enteignet, diesmal nach dem Denkmalschutzgesetz.
Bei der oben genannten Tagung wurde auch festgestellt, dass gar kein DDR-Mathematiker für einen
Vortrag nominiert war.
E. Brieskorn meldete sich zu Wort mit dem Vorschlag, er würde gern einen Beitrag von
Herrn Holzapfel hören. Ich selbst bemerkte, dass ich gerade gut präpariert sei.
Der Vorschlag wurde angenommen. Gut beurteilt wurde der Vortrag – wie ich später
erfuhr – von verschiedenen Seiten (auch USA). Meine Preprints wurden alle mitgenommen.
Ich erhielt von da an regelmäßig Einladungen zur Bonner Arbeitstagung, konnte diese
allerdings nicht annehmen. Die erste Gelegenheit hatte ich erst 1988 als ein leichtes
Tauwetter in den Ost-West-Beziehungen einsetzte. Hirzebruch erzählte mir, dass er sich selbst mit
einem Doktoranden bereits Mitte der 1970er Jahren an meinem Thema versucht hätte.
Aber es kam damals nichts dabei heraus.
Ein paar Mal kam Hirzebruch noch in den 1980ern in die DDR, erkundigte sich nach meinen Fortschritten,
richtete auch ein/zwei Seminar-Vorträge in Bonn darüber ein, die zu einer Bonner Dissertation
über „Picardsche Modulräume“ führten.
Nach der Wende wurde die Akademie der Wissenschaften der DDR abgewickelt.
Evaluiert wurde unsere Forschungsgruppe Zahlentheorie und Algebraische Geometrie von
Günter Harder vom MPIM in Bonn.
Wir – H. Koch,
Ernst-Wilhelm Zink
und ich – wurden für einen Zeitraum von (höchstens) fünf Jahren
zur „Max-Planck-Gruppe“ an der Berliner Humboldt-Universität erklärt.
Bis zu unserer Berufung auf Professorenstellen wurden wir aber noch direkt vom MPIM alimentiert.
Eine Zusammenkunft im Jahr 1991 mit F. Hirzebruch in einer Villa in Berlin-Grunewald legt nahe,
dass wir ihm diesen Weg zu verdanken haben.
Übrigens war auch G. Harder (1995-2006) nach Hirzebruchs Emeritierung Direktor des MPIM.
Juri Iwanowich Manin (*1937)
Juri Iwanowich Manin (Moskau) wurde im Jahr
1995 zum Kodirektor des MPIM berufen und blieb dies zehn Jahre lang. Fachlich bekannt war er mir
durch sein Buch „Kubicheskije Formi“ und seines Beweises der Mordell-Vermutung für
Funktionenkörper mit Hilfe des Gauß-Manin-Zusammenhanges.
Persönlich lernte ich ihn in einem Kinderferienlager der DDR kennen. Dort fand eine gut
besetzte Internationale
Konferenz mit
Teilnehmern aus Ost und West statt.
Aus Kostengründen wurde ein Kinderferienlager in Garwitz (bei Parchim, Mecklenburg) außerhalb
der Ferienzeit mitsamt Personal herangezogen.
Das wäre sicher auch heute eine gute Idee für klamme Kommunen zwecks besserer Einbindung
in den Wirtschaftskreislauf.
Anlässlich einer Arbeit, die ich für die neu gegründete Fachzeitschrift Annals of
Global Analysis and Geometry einreichte, wurde ich ihm vorgestellt. Er lobte den Schreibstil und
den hohen Anteil von Arithmetik, der in dem geometrischen Thema steckte. Auch, dass ich die
Fortsetzung einer Moskauer Dissertation in Angriff genommen hatte, fand er sympathisch.
Er bat mich, ihn – vor dem Heimflug – auf einen Abstecher nach Berlin zu begleiten.
Wir besuchten, auf seinen Wunsch hin, auch das Pergamon-Museum. Es ergaben sich interessante Gespräche
über Mathematik und die über die Stadt. Ihn interessierte z. B. wie ich auf
„Picardsche Modulflächen“ als Name für meine Forschungsobjekte gekommen bin.
Émile Picard entdeckte 1883 die Monodromie-Gruppen Γ von Lösungen spezieller
Differentialgleichungen über dem Innern des komplex-zweidimensionalen Einheitsballs
B:={(z1, z2)||z1|2
+ |z2|2 < 1} .
Die Basisfläche der Lösungsfunktionen kann als Modulfläche zugehöriger
Kurvenfamilien interpretiert werden. Auch interessierte er sich für M. Rapoport: Warum kann er –
aus der DDR kommend – West-Europa und Amerika besuchen, während wir solche Einladungen
nicht annehmen dürfen. Die Sache war – auf Rapoports österreichische
Staatsangehörigkeit verweisend – schnell erklärt.
Durch meinen Wechsel zur Akademie im Jahr 1979 konnte ich auch am Akademie-Austausch-Programm mit der UdSSR
teilnehmen. Der erste vierteljährige) Aufenthalt führte mich nach Moskau,
wo ich sofort für einen Vortrag in die Lomonossow-Universität zum Vinberg-Seminar eingeladen wurde.
Ich traf J. Manin am Steklov-Institut wieder. Er lud mich zu sich nach Hause ein, was ich als
besondere Ehre empfand. Wieder gab es wertvolle Ratschläge zu meinem Buch über
“Eulersche partielle Differentialgleichungen“, an dem ich arbeitete.
Ich erinnere mich an ein Gespräch über den sowjetischen Schriftsteller und Nobelpreisträger
Boris Pasternak (Dr. Schiwago). Eingangs eines von Manins Büchern wird Pasternak namentlich
erwähnt. „Warum wird er aber von der Sowjetführung bekämpft?“ fragte ich.
„Es gibt keinen vernünftigen Grund,“ antwortete er mir „denken Sie an Heinrich Heine
zu dessen Lebzeiten.“ Es war eine Analogie, die ich verstehen konnte.
Infolge (auch) von Manins Hinweisen, z. B. auf Delignes Hyperkohomologie-Gruppen und -Garben,
konnte ich die erste Euler-Vorlesung am Zentral-Institut für Mathematik und Mechanik der Akademie
(ZIMM) halten, die erwähnte Monographie „Geometry and Arithmetic Around Euler Partial
Differential Equations“, die beim VEB Deutscher Verlag der Wissenschaften und auch beim
niederländischen Reidel-Verlag erschien, fertigstellen und damit die Leonhard-Euler-Medaille gewinnen.
Gerd Faltings (*1954)
Gerd Faltings wurde als erstem deutschen
Mathematiker die Fields-Medaille verliehen, und zwar im Jahre 1986 für den Beweis der
Mordell-Vermutung im Jahr 1983:
Satz von Faltings: Jede (komplexe kompakte) glatte Kurve, die über einem
Zahlkörper K definiert ist, hat höchstens endlich viele K-Punkte, wenn ihr
Geschlecht > 1 ist.
Ich kannte G. Faltings persönlich von Konferenzen zu Beginn der 1980er Jahre.
Bei einer dieser Konferenzen in Rumänien unternahmen wir einen gemeinsamen Spaziergang.
Er erkundigte sich über meine Arbeit und die einiger Moskauer Kollegen. Speziell Manin,
Shafarevich, Parshin näherten sich dem Beweis der ca. 60 Jahre alten Mordell-Vermutung.
Ich merkte gleich, dass es sich bei Faltings um einen hochtalentierten Mathematiker handelt.
Im Vorfeld der Konferenz zur Algebraischen Geometrie in Bukarest 1983 wurde schon über das
bemerkenswerte Resultat von Faltings gemunkelt. Sein Vortrag war dann gewissermaßen die
Auslandspremiere des Beweises der Mordell-Vermutung.
Persönlich schenkte er mir sein 40-seitiges Preprint mit dem Beweis.
Ich passte nicht gut darauf auf, und es wurde mir geklaut, musste es dann von zu Hause aus noch
einmal bestellen. Zurück zur Tagung: Ich habe sie in starker Erinnerung, sowohl in
mathematischer als auch in menschlicher Hinsicht. Wir sangen gemeinsam fröhlich abends auf
der Konferenz-Party, z. B. „We shall overcome“. Ich stimmte zur Melodie von
„It's a long way to Tipparary“ die mathematische Variante
"It's a long way to blow down threefolds, it's a long way but we blow“.
Mehrere solcher Beiträge wurden nun angestimmt und mitgesungen –
„Long way to prove conjectures“ war auch nicht schlecht.
Nach Verleihung der Fieldsmedaille 1986 wurde ich vom Fachkollegen
Reinhard Bölling zur
Heinrich-Hertz-Schule eingeladen. Bölling leitete dort den Spezialkurs für die
algebra-interessierten Schüler. Mein Themenkreis enthielt natürlich: Mordell-Vermutung,
Fields-Medaille und meine Bekanntschaft mit G. Faltings. Es war das einzige Mal,
dass ich direkten Kontakt zum Heinrich-Hertz-Gymnasium hatte.
Faltings ging 1985-1994 als Professor nach Princeton. Im folgenden Jahr kehrte er zurück
nach Deutschland. Seitdem ist er Kodirektor des MPIM in Bonn.
Peter Scholze (*1987)
Wissenschaftliche Biographie
Peter Scholze wurde im Jahre 1987 in Dresden geboren, wuchs aber in Berlin auf und besuchte das
durch sein mathematisches Profil geprägte Heinrich-Hertz-Gymnasium in Berlin-Friedrichshain.
Von seinem sechzehnten Lebensjahr an wurde er durch Professor
Klaus Altmann
an der Freien Universität Berlin gefördert. Nach kurzer Zeit nahm er auch an Mathematikseminaren
dieser Universität teil. In einer e-Mail schrieb er: „Meine Zeit an der Heinrich-Hertz-Schule
war für mich prägend, und hat sehr zu meiner Entwicklung beigetragen.
Der Einfluss der Schule erstreckt sich über meine gesamte mathematische Laufbahn,
von den ersten Anfängen bei der Mathematikolympiade, die ich ohne die Vorbereitung in den AGs an
der Schule nicht so erfolgreich gemeistert hätte, über die ersten Vorlesungen an der
Universität, die ich bereits während der Schulzeit bei Professor Klaus Altmann,
ehemaliger Hertz-Schüler, besuchen konnte.“ Peter Scholze legte im Jahr 2007 am
Heinrich-Hertz-Gymnasium sein Abitur mit der Durchschnittsnote 1,0 ab.
Im Mathematikunterricht arbeitete Peter immer zweigleisig. Einerseits verfolgte er das
Unterrichtgeschehen mit halbem Ohr und griff in die Diskussion ein, wenn ihm irgendwas nicht recht
gefiel oder wenn die Lösung des Problems zu lange auf sich warten ließ.
Er schüttelte dann Lösungsvorschläge aus dem Ärmel und konnte diese –
zumeist lächelnd – an der Tafel sofort sauber und verständlich für alle
darstellen. Andererseits war Peter im Unterricht immer in mathematische Fachliteratur vertieft
oder löste Aufgaben
Mathematik-Olympiade
höherer Stufen. Nachmittags besuchte Peter dann
Mathematik-Arbeitsgemeinschaften an der Schule oder Veranstaltungen der
Mathematischen Schülergesellschaft
„Leonhard Euler“ an der Humboldt-Universität.
„In der 11., 12. und 13. Klasse konnten wir als Heinrich-Hertz-Schule unserem Peter mathematisch
nicht mehr allzu viel bieten. Da kam uns unser ehemaliger Schüler, Prof. Dr. Klaus Altmann
(Absolvent unserer Schule 1975) zu Hilfe. Peter wurde von Klaus Altmann in der 11., 12. und 13.
Klasse individuell an der Freien Universität Berlin betreut und besuchte unseren profilierten
Mathematik-Leistungskurs nur noch sporadisch. Während dieser Betreuungszeit begann Peter
ernsthaft und systematisch auf dem Gebiet der algebraischen Geometrie zu arbeiten.“
Mit 16 erfuhr Peter Scholze, dass zehn Jahre zuvor
Andrew Wiles das berühmte
Fermatsche Problem
aus dem 17. Jahrhundert gelöst hatte: Man beweise, dass die Gleichung
xn+yn = zn keine Lösung in natürlichen
Zahlen hat, wenn der Exponent n größer als 2 ist.
Scholze wollte den Beweis verstehen, musste aber bald feststellen, dass zwar die Aufgabe einfach zu
formulieren ist, aber die Lösung allerlei von der härtesten aktuellen Mathematik erfordert:
„Ich begriff erst mal gar nichts, aber es war faszinierend.“
Daraufhin arbeitete sich der Schüler von hinten nach vorne durch das Material:
Jedes Mal, wenn er etwas nicht verstand, eignete er sich den dazu erforderlichen Stoff an,
dann das, was man brauchte, um diese Inhalte zu verstehen, und so weiter.
„Ungefähr so lerne ich heute noch“, erklärt er im Gespräch.
„Was man in der Anfängervorlesung macht, wie Lineare Algebra, habe ich nie richtig
studiert das habe ich bei anderen Gelegenheiten nebenher mitbekommen.“
Von seinem achtzehnten Lebensjahr an wurde er durch Michael Rapoport, Professor für
arithmetische algebraische Geometrie an der Rheinischen Friedrich-Wilhelms-Universität Bonn,
gefördert, wo er innerhalb von fünf Semestern das Studium mit dem Master-Abschluss
absolvierte. Im Jahre 2012 wurde Scholze mit seiner Dissertation unter dem Titel
„Perfectoid Spaces“ promoviert. Zum Wintersemester 2012/13 wurde er auf eine der
Hausdorff-Professuren für
Mathematik beim Exzellenzcluster in Bonn berufen. Sein Fachgebiet ist die
arithmetisch-algebraische Geometrie mit dem Langlands-Programm als speziellen Rahmen.
2018 wurde er zu einem der Direktoren des Max-Planck-Instituts für Mathematik ernannt.
Auf dem Weg zur Fieldsmedaille 2018
Sein bislang bedeutendstes Konzept ist eine Klasse fraktaler Strukturen, die er
Perfektoide Räume genannt hat. Die Idee ist erst ein paar Jahre alt,
hat aber bereits reiche Früchte in der algebraischen Geometrie getragen.
Die entdeckten Räume sind zwar sehr groß und komplex, haben aber für viele Probleme
nützliche geometrische Eigenschaften. Mit ihrer Hilfe konnten inzwischen eine ganze Reihe von
alten schwierigen Problemen der Zahlentheorie gelöst werden.
In den 1970er Jahren hatten die Mathematiker bemerkt, dass den p-adischen Zahlen leichter
beizukommen ist, wenn man nicht nur sie selbst studiert, sondern auf ihnen einen unendlichen Turm
von Zahlensystemen aufbaut: zuunterst die p-adischen Zahlen selbst, darüber ein System
aus p im Kreis angeordneten Exemplaren der p-adischen Zahlen, und so weiter:
Jedes Stockwerk ist in einem gewissen Sinn eine p-fache Version des unmittelbar unter ihm
liegenden.
Mit anderen Worten sind Perfektoide Räume 'Unendliche Türme' aus immer
größeren Zahlensystemen. Die Hauptrolle spielen dabei die p-adischen Zahlen.
„Inzwischen bin ich sie so gewohnt, dass mir die reellen Zahlen komisch vorkommen“,
sagte Scholze in einem Interview.
Im Jahr 2010 ging ein Gerücht unter den Zahlentheoretikern um. Angeblich hatte ein Student
aus Bonn eine Arbeit geschrieben, die auf nur 37 Seiten erledigte, wofür die beiden etablierten
Wissenschaftler
Michael Harris und
Richard Taylor ein Buch von immerhin 288 Seiten gebraucht hatten:
den bis zur Undurchdringlichkeit verwickelten Beweis eines Satzes aus der Zahlentheorie,
der wiederum von einem Spezialfall der berühmten Langlands-Korrespondenz handelt.
Tatsächlich – der 22-jährige Peter Scholze hatte in seiner Masterarbeit
einen der kompliziertesten Teile des Beweises durch eine elegante Eigenkonstruktion ersetzt.
Mitte des 20. Jahrhunderts entdeckten die Mathematiker (insbesondere auch
Robert Langlands10))
eine Beziehung der Reziprozitätssätze zu einem anscheinend völlig anderen Thema:
der hyperbolischen Geometrie.
Die Verbindung zwischen den Reziprozitätssätzen und der hyperbolischen Geometrie ist ein
Kernstück des oben genannten Langlands-Programms, einer Sammlung von Sätzen und
Vermutungen, die Zahlentheorie, Analysis und Geometrie miteinander verbinden. Einmal bewiesen,
erlauben die Vermutungen weitreichende Folgerungen. So ist es möglich, den Beweis von
Fermats letztem Satz auf einen kleinen, allerdings alles andere als einfachen Teil des
Langlands-Programms zurckzuführen.
In dem Überblicksartikel „p-adic Geometry“, den P. Scholze für den
vorjährigen Internationalen Mathematikerkongress in Rio de Janeiro geschrieben hat,
fasst er nicht nur seine Forschungen über die seltsame und reichhaltige Welt der
p-adischen Strukturen zusammen. Er beschreibt auch deren Beziehungen zur berühmten
Langlands-Korrespondenz.
Hiermit wurden wir – auch wenn wir vieles nur ansatzweise verstehen –
Zeugen eines wissenschaftlichen Vulkanausbruchs, dessen Schwelen 120 Jahre zuvor mit der Erfindung
der p-adischen Zahlen durch Kurt Hensel in Berlin begann.
Pressestimmen im August 2018
Der SPIEGEL nennt P. Scholze in einem Artikel seiner letzten Juli-Ausgabe den
„Mozart der Mathematik“. Er wird als Mathematik-Forscher der entlegendsten Sphären
der Zahlentheorie vorgestellt. Von seinen Kollegen wird er als freundlich, bodenständig, jederzeit
ansprechbar gelobt. So einen Mathematiker wie ihn gibt es nur alle paar Jahrzehnte einmal, meint sein
Doktorvater M. Rapoport, selbst ein Großmeister seines Fachs. Scholze ist auf der Höhe der
Abstraktion unterwegs, in der anderen Fachkollegen einfach die Luft zu dünn wird,
in einer Todeszone gewissermaßen. Als Student von 22 Jahren nahm Scholze eine Vermutung in
Angriff, die als „lokale Langlands-Korrespondenz“ bekannt ist. Es geht dabei um das
Verwandeln von Zahlensystemen in geometrische Gebilde, die dann einen leichteren Zugriff
ermöglichen.
Schon in seiner Zeit auf dem Heinrich-Hertz-Gymnasium las er nebenher schwierige Fachbücher.
Dem Unterricht folgte er nur mit halbem Ohr, so berichten seine dortigen Lehrer.
Auch schrieb er schon damals nie mit. Bis heute macht Scholze fast alles im Kopf.
Wenn er sich mal zwingt mitzuschreiben, kriegt er nichts mit, erklärte er.
Er wird in dieser Beziehung mit Mozart verglichen, der schon mal eine Oper vollständig im Kopf
komponierte und sie danach erst aufschrieb. Mir, dem Autor, fällt auch in diesem Zusammenhang
Henri Poincaré ein, der eine Vorlesung nur vom Zuhören her, ohne –
wegen einer Sehschwäche – das Tafelbild zu erkennen, vollständig rekonstruieren
konnte.
Auf der Titelseite des BERLINER KURIERs erscheint am 2. August 2018 unter der Überschrift
„Berlins klügster Kopf, Genie Ost“ die Zeile: Peter Scholze (30) gewinnt die weltweit
bedeutendste Auszeichnung für Mathematiker – und sagt: „Zu verdanken habe ich das auch
dem Schulsystem der DDR.“ Auf der Textseite findet man die verkorkste Kopfzeile: Top-Preis für
Rechen-Genie aus Berlin. Und weiter in journalistischer Wortspiel-Manier: Unter seiner Matte gibt's
mehr als Mathe.
In einem Brief an seine ehemalige Heinrich-Hertz-Schule schreibt er:
„Ich hoffe, dass auch künftige Generationen das Glück haben, in einem Netzwerk von
mathematisch und naturwissenschaftlich herausragenden Schulen unterrichtet zu werden“.
Auch DIE WELT vom 2. August bringt sein Konterfei auf's Titelblatt mit Hinweis auf ein Interview
auf Seite 28. Dort erzählt er: „Meine ganze Kraft fließt in die Mathematik.“
Er hat den Charme eines jungen Studenten und zählt doch zu den genialsten Mathematikern unserer
Zeit. Im Kinderbuch „Fregattenkapitän Eins“ fand er seine erste Berührung mit
der Mathematik. Weiter sagt er: „Es macht keinen Sinn diese noch ungelösten Probleme
einfach mal so angreifen zu wollen. Dafür sind sie einfach zu schwierig. Nur wenn man ohnehin
zu einer neuen Erkenntnis gelangt ist, die möglicherweise ein Schlüssel zur Lösung
eines dieser Probleme sein könnte, gibt es eine Chance. Nur dann wäre es sinnvoll,
es zu probieren.“
Scholze kennt auch das Gefühl des Scheiterns, wenn man nach wochenlanger Arbeit zu keinem
Ergebnis gekommen ist. „Noch schlimmer ist es, wenn man geglaubt hat, den Beweis gefunden zu
haben, und dann nach einem Monat feststellen muss, dass die Sache doch nicht funktioniert.
Das ist schon frustrierend.“
„Für mich fühlt es sich so an, dass ich die Mathematik entdecke.
Mein Zugang ist da in gewisser Weise ein naturwissenschaftlicher. Ich versuche Strukturen zu
verstehen, die bereits objektiv da sind. Dabei habe ich gar keine Wahl, wie ich die Dinge angreifen
kann. Es wird mir von der Sache vorgegeben, was ich zu tun habe.“
„Mein Vorbild ist der 2014 verstorbene Mathematiker Alexander Grothendieck.
Er hat die algebraische Geometrie auf ein neues Fundament gestellt und die Voraussetzungen für
meine Arbeiten geschaffen."
Abschließend
Erica Klarreich: „Mit gerade einmal
30 Jahren hat Peter Scholze ein ganzes Fachgebiet umgekrempelt. Dafür erhält er die
Fields-Medaille der Mathematik 2018.“
Echo einiger internationaler Kollegen
Jared Weinstein, Zahlentheoretiker an
der Boston University:
Es war einfach unglaublich, dass jemand in so jungem Alter etwas so Revolutionäres zustande
bringt. Er kann die Entwicklungen sehen, bevor sie überhaupt angefangen haben;
er hat Hellseher-Qualitäten. Das Verrückteste an den perfektoiden Räumen ist,
dass man mit ihnen auf wundersame Weise von einem Zahlensystem zum anderen wechseln kann.
1970 formulierte Pierre Deligne seine „weight-monodromy conjecture“.
Mit dem Beweis promovierte P. Scholze 2012 – und seine Dissertation hatte so
weitreichende Folgen, dass Arbeitsgruppen auf der ganzen Welt sich in sie vertiefen.
Perfektoide Räume sind zweifellos etwas vom Schwierigsten überhaupt in der Mathematik.
Gleichwohl ist Scholze bekannt für die Klarheit seiner Darstellungen, in Artikeln wie in
Vorträgen. Ich verstehe gar nichts, bis Peter es mir erklärt. Während sich die
Fachkollegen auf der ganzen Welt mit den perfektoiden Räumen herumschlagen, stammen die
weitreichendsten Entdeckungen auf diesem Gebiet, wenig erstaunlich, von Scholze selbst und seinen
Arbeitskollegen. Ein Ergebnis, das er 2013 ins Internet stellte, erregte ungläubiges Erstaunen
bei der Fachwelt. Wir hätten nie gedacht, dass ein derartiger Satz überhaupt in Reichweite war.
In dieser Arbeit gelang es Scholze, die so genannten Reziprozitätssätze zu verallgemeinern.
Dabei geht es um Polynomgleichungen in modularer Arithmetik. Man kann größere Teile der
modernen algebraischen Zahlentheorie als den Versuch auffassen, diese Gesetze zu verallgemeinern.
Bhargav Bhatt von der University of
Michigan:
Nach wie vor arbeitet Scholze an den perfektoiden Räumen; aber inzwischen hat er einen Ausflug
zur algebraischen Topologie unternommen, das ist die Fachrichtung, die deformierbare Gebilde mit
Mitteln der Algebra untersucht. In nur anderthalb Jahren ist er zum absoluten Experten auf diesem
Gebiet geworden. Die Fachkollegen sehen es mit einer Mischung aus Furcht und Begeisterung,
wenn Scholze ihr Reich betritt. Das heißt, dass in naher Zukunft viel passieren wird.
Man wird den Grenzen der Erkenntnis beim Wandern zusehen können.
Eugen
Hellmann (Ex-Kommilitone):
Es liegt an seiner phänomenalen Fähigkeit, tief in das Wesen eines mathematischen
Gegenstands zu blicken. Anders als viele seiner Fachkollegen nimmt er sich nicht die Lösung
eines speziellen Problems vor, sondern ein rätselhaftes Konzept, das er um seiner selbst willen
verstehen möchte. P. Scholze hat nie etwas mitgeschrieben. Er hat das auf der Stelle verstanden,
und nicht bloß irgendwie, sondern so tief durchdrungen, dass er es nie wieder vergaß.
Scholze hat die klarste Form gefunden, in der man alle bisherigen Ergebnisse ausdrücken konnte,
und das auf elegante Weise und weil das genau die richtige Begriffsbildung war, konnte er weit über
das bisher Bekannte hinausgehen. Selbst mit einer Einführung durch Scholze sind perfektoide
Räume alles andere als einfach zu verstehen. Wenn du auch nur ein bisschen von dem Weg abweichst,
den er vorgibt, landest du im finstersten Dschungel, und dann wird's richtig schwierig.
Aber Peter steckt niemals im Dschungel fest. Er versucht sich gar nicht erst durchzuschlagen.
Er fliegt drüber. Es war wie ein Flug über den bisherigen Dschungel.
Ana Caraiani, Zahlentheoretikerin am
Imperial College London:
Hinterher finden die Strukturen, die er sich ausgedacht hat, Millionen von Anwendungen,
die vorher niemand erahnen konnte, eben weil es genau die richtigen Konzepte waren.
Scholze ist sich nicht zu schade, seine Ideen auf Vordiplomsniveau zu erläutern.
Dank seiner freundlichen, zugänglichen Art ist er die ideale Führungspersönlichkeit auf
seinem Gebiet.
Bildnachweis
| Porträt von Kurt Hensel um 1925 | Dieses Porträt ist gemeinfrei, Quelle ist https://de.wikipedia.org/wiki/Kurt_Hensel#/media/File:Hensel_Kurt.jpg | |
| Titelblatt | eingescannt | |
| Porträt von Helmut Hasse | Konrad Jacobs, mit freundlicher Genehmigung vom Bildarchiv des Mathematischen Forschungsinstituts Oberwolfach | |
| Porträt von Hans Reichardt | Heinz Schadewald, mit freundlicher Genehmigung der Humboldt-Universität Berlin, Quelle: Porträtsammlung Berliner Hochschullehrer, Foto, Porträt, Hans Reichardt | |
| Porträt von Emmy Noether | Urheber ist unbekannt. Dieses Porträt ist gemeinfrei, Quelle ist https://commons.wikimedia.org/wiki/File:Noether_retusche_nachcoloriert.jpg. Es ist zu vermuten, dass das Kolorieren durch Kämpel durchgeführt wurde. | |
| Porträt von Heinrich Grell | Die Fotografie ist der Oberwolfach Photo Collection entnommen, Quelle ist https://owpdb.mfo.de/detail?photo_id=1427. Sie darf gemäß der Creative Commons License Attribution-Share Alike 2.0 Germany verwendet werden. | |
| Schreiben von H. Grell | Scan des Originals | |
| Lothar Budach | aus dem Fundus des Autors | |
| Urkunde | Scan des Originals | |
| M. Rapoport und R.-P. Holzapfel | aus dem Fundus des Autors | |
| Spezialschulen | Bildschirmabzug (Screenshot) von der Grafik auf Wikipedia-Seite Spezialschule mathematisch-naturwissenschaftlich-technischer Richtung | |
| M. Rapoport und Th. Zink | aus dem Fundus des Autors | |
| Porträt von Friedrich Hirzebruch | Die Fotografie ist der Oberwolfach Photo Collection entnommen, Quelle ist https://owpdb.mfo.de/detail?photo_id=12837. Sie darf gemäß der Creative Commons License Attribution-Share Alike 2.0 Germany verwendet werden. | |
| Schloss Reinhardsbrunn | Rolf-Peter Holzapfel, Bernau | |
| Porträt von Günter Harder | Die Fotografie ist der Oberwolfach Photo Collection entnommen, Quelle ist https://owpdb.mfo.de/detail?photo_id=10793. Sie darf gemäß der Creative Commons License Attribution-Share Alike 2.0 Germany verwendet werden. | |
| Titelblatt des Vorabdrucks der Euler-Vorlesung 1982 | Scan des Originals | |
| Porträt von Gerd Faltings | Die Fotografie ist der Oberwolfach Photo Collection entnommen, Quelle ist https://owpdb.mfo.de/detail?photo_id=7513. Sie darf gemäß der Creative Commons License Attribution-Share Alike 2.0 Germany verwendet werden. | |
| Porträt von Peter Scholze | Die Fotografie ist der Oberwolfach Photo Collection entnommen, Quelle ist https://owpdb.mfo.de/detail?photo_id=20858. Sie darf gemäß der Creative Commons License Attribution-Share Alike 2.0 Germany verwendet werden. |
1) ≪ bedeutet, dass i höchstens endlich viele
negative Werte in der Summe annimmt.
2) Ideen zu Analogien zwischen Zahl- und Funktionenkörpern
gehen auf Richard Dedekind (1831-1916) und
Rudolf Heinrich Weber (1874-1920) zurück.
Eine gemeinsame Sprache wird mit dem Begriff des Stellenringes vom deutschen Algebraiker
Wolfgang Krull (1899-1971) gefunden
für Ringe der Taylor-Reihen in (1) bzw. (2).
Später führte dies zur einheitlichen arithmetisch-geometrischer Behandlung mit Hilfe von
Grothendiecks Schema-Theorie (s. u.??).
3) Es werden hier die in der DDR offiziell verwendeten
Begriffe verwendet. Die Graduierung zum Doktor der Wissenschaften entspricht der Habilitation
ohne Lehrbefähigung, die Aspirantur bezeichnet die Fortsetzung des Studiums zum Erwerb eines
weiteren akademischen Grads (vergleiche die Wikipedia-Artikel
Akademischer Grad und
Aspirantur).
4) Ich habe auch ein
Filmchen gedreht von einem Wandertag der Seminargruppe
an den Stienitzsee (nahe Wandlitz), den ich inzwischen digitalisiert habe. Er enthält wertvolle
Aufnahmen mit Grell, Budach, Kollegen und Studenten.
6) Heute müsste man im Hinblick auf die Entwicklungen z. B. in
China und den USA neu darüber nachdenken.
7) Inge Rapoport: Meine ersten drei Leben, NORA-Verlag, 1997, S. 330ff
8) Es waren drei, vergessen wurde Gerd Siebert.
9) Deutschsprachiger Bezug: https://de.wikipedia.org/wiki/Hans_Reichardt
10) Gewinner des Abelpreises 2018