Mathematiker des Monats August 2024
Ernst Kossak (1839-1892)
von
Peter Ullrich
Am 1. April 1879 wurde die heutige
Technische Universität Berlin unter dem Namen
„Königlich Technische Hochschule zu Berlin“ in Charlottenburg gegründet
(im Folgenden kurz: TH Charlottenburg) unter Zusammenlegung der
Berliner Bauakademie und der
Königlichen Gewerbeakademie.
(Die Bergakademie Berlin kam
erst am 1. Oktober 1916 hinzu.) Bereits an diesen Vorgängerinstitutionen war die Mathematik
personell vertreten, sogar mit insgesamt vier etatmäßigen Professuren.
Ernst Kossak als einer der Vertreter für
Höhere Mathematik an der Gewerbeakademie war einer dieser
Gründungsprofessoren der Mathematik an der TH Charlottenburg.
Weiterhin ist Kossak als Verfasser der ersten veröffentlichten Darstellung der von
Karl Weierstraß (1815-1897) entwickelte Version des
Begriffs der Zahl, insbesondere der reellen Zahl, bekannt.
Auch Kossaks weitere Publikationen beschäftigen sich mit einer Thematik,
der Weierstraß sogar noch näher stand, nämlich der Theorie der elliptischen und
ultra-elliptischen Funktionen, also Spezialfällen der Abel'schen Funktionen.
Man könnte somit vermuten, Kossak sei der Weierstraß'schen Schule in der Mathematik
zuzurechnen.
Dies ist jedoch nicht der Fall: Sowohl sein Staatsexamen als auch seine
Promotion legte er nicht in Berlin ab; allein die Habilitation fand an diesem Orte statt,
aber auch bei dieser sind Überraschungen zu vermelden.
Leben
Zunächst sei darauf hingewiesen, dass ungefähr zeitgleich mit dem Mathematiker
Ernst Kossak (1839-1892) auch ein Journalist namens Ernst Kossak (1814-1880) lebte,
welcher als Vater des Berliner Feuilletons im 19. Jahrhundert gilt.
Beide lassen sich zum einen durch ihre weiteren Vornamen unterscheiden,
beim Mathematiker „August“ und „Martin“, beim Journalisten
„Karl“ und „Ludwig“.
Zum anderen haben sie unterschiedliche Geburtsjahre,
wobei allerdings für den Mathematiker bisweilen auch fälschlich das Geburtsjahr 1807
angegeben ist.
Jugend und Studienzeit
Der spätere Mathematiker Ernst (August Martin) Kossak wurde am 16. Januar 1839
in Friedland in Ostpreußen geboren (heute: Prawdinsk, Oblast Kaliningrad, Russland),
weniger als 50 Kilometer von Königsberg entfernt. Seine Eltern waren der Bürgermeister
Ludwig Kossak und dessen Ehefrau Franziska, geborene Wittcke. Zunächst ging Kossak in
Friedland zur Schule; ab 1853 besuchte er das Gymnasium in Konitz, das er allerdings im
Dezember 1857 als Primaner verließ, um Maschinenbau zu studieren. Nach einiger Zeit
jedoch kehrte er an das Gymnasium zurück, legte 1859 die Reifeprüfung ab und studierte
danach an der Universität in Königsberg Mathematik und Physik.
Den Berichten über sein Leben zufolge wurde Kossak dabei hauptsächlich von den
beiden Ordinarien
Friedrich Richelot
(1808-1875) in der Mathematik und
Franz Neumann (1798-1895)
in der Physik geprägt. Jedoch hörte er auch Vorlesungen bei
Eduard Luther (1816-1887, Astronomie),
Ludwig Moser (1805-1880, Physik),
Georg Rosenhain (1816-1887,
Mathematik) und
Karl Rosenkranz (1805-1879, Philosophie).
Insbesondere bauen Kossaks Arbeiten über elliptische und ultra-elliptische Funktionen
auf Rosenhains 1851 veröffentlichter Pariser Preisschrift
„Mémoire sur les fonctions de deux variables, qui sont les inverses des
intégrales ultra-elliptiques de la première classe“ auf.
(Allerdings hatte Rosenhain zur Studienzeit Kossaks seine mathematisch produktive Phase
bereits hinter sich, so dass man spekulieren kann, ob es auch die Vorlesungen oder
nur die Schriften Rosenhains waren, die Kossak inspirierten.)
Seine schriftliche Prüfungsarbeit für das Staatsexamen jedenfalls verfasste Kossak
1864 über das von Rosenhain bereits in seiner Preisschrift behandelte Thema des
Additionstheorems für ultra-elliptische Integrale erster Ordnung, eine Arbeit,
die Richelot in seinem Abschlusszeugnis vom 1. April 1865 als wissenschaftlich bedeutsam lobte.
Lehrer in Berlin
Zwar legte Kossak sein Staatexamen für das Lehramt an Gymnasien in den Fächern
Mathematik und Physik in Königsberg ab, promovierte dort aber nicht.
Stattdessen wechselte er im Frühjahr 1865 nach Berlin, wo er sein Probejahr als Lehrer,
also die damalige Entsprechung des Vorbereitungsdienstes, an der
Dorothenstädtischen
Realschule begann, von der er noch zum Oktober des gleichen Jahres an das
Friedrichswerdersches
Gymnasium1) wechselte, an dem er auch im Anschluss
an das Probejahr eine feste Stelle erhielt und bis 1873 als Lehrer wirkte.
Diese Tätigkeit schien ihn jedoch nicht voll auszufüllen:
Zum einen besuchte er im Wintersemester 1865/66 die einführende Vorlesungsreihe
„Principien der Theorie der analytischen Functionen“ von Weierstraß.
Zum anderen suchte und fand er nebenamtliche Tätigkeiten an anderen Bildungseinrichtungen.
So unterrichtete er vom 1. Oktober 1868 bis zum 30. September 1869 das Fach Physik
an der Kriegsakademie in Berlin.
Habilitation
Vor allen Dingen aber legte Kossak im Herbst 1869 die Habilitation im Fach Mathematik
an der Berliner Gewerbeakademie ab. Dies ist zum einen überraschend,
weil Kossak zu jenem Zeitpunkt (noch) nicht promoviert war,
was an Universitäten die übliche Voraussetzung für diese Art der Prüfung war
und ist. Grundsätzlich mag zum anderen auch verwundern, dass die Gewerbeakademie
überhaupt das Habilitationsrecht besaß:
Der TH Charlottenburg als ihrer Nachfolgeinstitution wurde das Promotionsrecht erst 1899
verliehen und dies auch zunächst nur für die Ingenieurwissenschaften;
das allgemeine Promotionsrecht – auch für das Fach Mathematik –
folgte erst 1924 nach, unter explizitem Hinweis auf die damals an der TH ausgebildeten
Lehramtsstudierenden.
Erklären lässt sich dies dadurch, dass im Rahmen der Humboldt'schen Bildungsreform
in Preußen Anfang des 19. Jahrhunderts die Habilitation als Eignungsnachweis für die
Lehrtätigkeit an Universitäten eingeführt worden war, sozusagen als Analogon
zum Lehramtsstaatsexamen, nur eben für den Tertiärbereich der
Bildung2).
In den darauffolgenden Jahrzehnten änderten einige berufspraktisch orientierte
Bildungseinrichtungen ihr Profil – von dem einer Berufsschule zu dem einer
akademischen Einrichtung.
Dies wurde beispielsweise nach außen hin dadurch sichtbar, dass das Berliner
„Gewerbeinstitut“, an dem Weierstraß von 1856 bis 1861 (formal bis 1864)
als Professor gewirkt hatte, am 14. April 1866 in „Gewerbeakademie“ umbenannt wurde.
Im Rahmen dieser Aufwertung erfolgte auch die Verleihung des Habilitationsrechts
am 1. März 1866 an diese Institution, die damit den Nachwuchs ihres Lehrkörpers selbst
regulieren durfte.
Man ließ sich dort jedoch Zeit mit dem Erlass einer Habilitationsordung:
Die Gewerbeakademie erhielt überhaupt keine, und selbst an der 1879 gegründeten
TH Charlottenburg dauerte es noch bis 1884, bis eine solche Ordnung erlassen wurde,
die die Promotion zur Voraussetzung machte. Insbesondere konnte Kossak also 1869
unpromoviert an der Gewerbeakademie habilitiert sowie dort Privatdozent werden und in dieser
Funktion Lehraufträge wahrnehmen.
Promotion
Dennoch schien Kossak irgendwann klar zu werden, dass eine Promotion von Vorteil sein könnte,
sei es für eine Schulkarriere, sei es für einen Wechsel zu einer hauptamtlichen
Tätigkeit an der Gewerbeakademie oder einer vergleichbaren Einrichtung.
Die Universität, die er sich zum Promovieren aussuchte, überrascht allerdings im ersten
Moment: Er hatte in Königsberg studiert, kannte dort also Professoren, und er hatte in Berlin
zumindest eine Vorlesung von Weierstraß gehört und Bekanntschaft mit einigen von dessen
Studenten geschlossen, beispielsweise mit
Hermann Amandus Schwarz (1843-1921).
Kossak wählte jedoch Göttingen als Promotionsort.
Über den Grund, warum Kossak nicht in Berlin promovierte, etwa bei Weierstraß,
der seit 1864 Ordinarius an der Universität war, also Promotionen begutachten durfte,
lässt sich nur spekulieren: Wahrscheinlich hätte Weierstraß erwartet,
dass Kossak vor einer Promotion seinen gesamten viersemestrigen Vorlesungskurs gehört
und auch durchgearbeitet hätte, nicht nur die einführende Vorlesung.
Vielleicht wollte Kossak aber auch kein Risiko hinsichtlich des Themas seiner Dissertation
eingehen:
Er beabsichtigte, die in seiner Staatsexamensarbeit aus dem Jahr 1864 schon dargestellten
Ergebnisse erneut zu beweisen, wenn auch mit anderen Methoden.
Das war an sich schon etwas angreifbar, hatte dazu aber noch den Nachteil,
dass der Weierstraß-Schüler
Leo Koenigsberger (1837-1921) Ende des Jahres 1864
eine Arbeit über dieses Thema publiziert hatte.
(Diese Hypothese wird dadurch gestützt, dass
Emil Lampe (1840-1918) in seinem Nachruf
auf Kossak zwar von der Promotion in Göttingen wusste, aber den Titel der Dissertation nicht
kannte: Einerseits behauptete er, die Dissertation sei nicht gedruckt worden; andererseits
führte er an anderer Stelle diese Schrift unter den Publikationen Kossaks auf.)
Gegen Königsberg hingegen sprach die Verpflichtung, eine bestimmte Zeit direkt vor
der Promotion dort als Student eingeschrieben gewesen zu sein, was Kossak aufgrund
seiner Tätigkeit als Lehrer am Friedrichswerderschen Gymnasium und Lehrbeauftragter an der
Gewerbeakademie nicht zu leisten im Stande war. Allerdings wirkten in Königsberg
Professoren, die enge Beziehungen nach Göttingen hatten:
Alfred Clebsch (1833-1872),
einer der Ordinarien in Göttingen, hatte von 1850 bis 1854 bei Richelot in
Königsberg studiert, und dieser hatte ja Kossaks Staatsexamensarbeit sehr gelobt.
Weiterhin war Rosenhain, auf den sich Kossak in seiner Arbeit bezog,
seit 1856 korrespondierendes Mitglied der Göttinger Gesellschaft der Wissenschaften,
Franz Neumann sogar auswärtiges.
Und die Promotionsordnung der Universität in Göttingen verzichtete nicht nur auf
die Pflichtsemester vor Ort – das tat übrigens auch die der Universität
Halle-Wittenberg (vergleiche den Fall der Promotion von
Hermann Schubert [1848-1911]) –,
sondern ließ sogar die Promotion in absentia zu,
dass man also überhaupt nur die Dissertation einzureichen und gar nicht vor Ort zu
erscheinen brauchte, nicht einmal zu einer mündlichen Doktorprüfung.
(Aufgrund der Tätigkeit von Autoren, die gegen Bezahlung Dissertationen anfertigten,
geriet diese Art der Promotion im letzten Drittel des 19. Jahrhunderts in Verruf.
Als Folge davon wurde in Frage gestellt, ob die Promotion der Weierstraß-Schülerin
Sofja Kowalewskaja [1850-1891]
in absentia 1874 in Göttingen überhaupt regulär erfolgt sei.
Kossaks Beispiel jedoch belegt, dass diese Art der Promotion noch wenige Jahre
davor dort gang und gäbe war. Möglicherweise war seine Promotion,
die in Berlin naturgemäß nicht unbekannt blieb, sogar die Blaupause für
Weierstraß, der die Promotion für Kowalewskaja organisieren musste,
die, im Gegensatz zu Kossak, zuvor kein reguläres Studium absolvieren konnte.)
Auf jeden Fall hatte Kossak offenbar intensiv vorgearbeitet,
als er am 31. Mai 1871 an die Philosophische Fakultät in Göttingen schrieb:
„meine gegenwärtige
amtliche Stellung als ordentlicher Lehrer am Werderschen Gymnasium in Berlin und als Privatdozent
an der Gewerbe-Akademie macht es mir erwünscht, die Promotion in absentia zu
erlangen.“
Auch die Geschwindigkeit der Begutachtung der immerhin 20 Seiten langen Dissertation
spricht dafür, dass Clebsch keinesfalls von der Einreichung überrascht wurde.
Bereits vier Tage später, am 4. Juni 1871, gab
Karl Hoeck (1794-1877) als Dekan der
Fakultät bekannt:
„Seine [= Kossaks]
eingereichte Abhandlung ,Das Additionstheorem der Abelschen Functionen' hat Herr College Clebsch
geprüft“,
so dass Kossak bereits am 31. August 1871 promoviert werden konnte, in absentia.
Professor an der Gewerbeakademie und an der TH Charlottenburg
Falls Kossak seine Promotion betrieben hatte, um seine Karrierechancen zu erhöhen,
so hatte er dies im richtigen Moment getan: Am Gewerbeinstitut hatte es schon sehr früh
Lehraufträge, Teilzeittätigkeiten und zuletzt sogar eine regelrechte Professur für
Geometrie, insbesondere Darstellende Geometrie gegeben. Im Wesentlichen für Weierstraß
persönlich war dann 1856 eine Professur für höhere Mathematik, insbesondere Analysis
geschaffen worden, auf der ihm vom Wintersemester 1861/62 ab vertretungsweise und ab
1864 endgültig
Siegfried Aronhold
(1819-1884) nachfolgte, der zuvor bereits Lehrer an der Berliner Bauakademie gewesen war.
Bereits 1868 hatte
Franz Reuleaux (1829-1905),
der damalige Direktor der Gewerbeakademie, die zuständigen Behörden davon überzeugt,
eine zweite Professur für höhere Mathematik einzurichten. Diese hatte zum 1. April 1869
Elwin Bruno Christoffel (1829-1900) angetreten.
Dessen Hoffnungen, wie zuvor Weierstraß auch Extraordinarius an der Universität in Berlin
zu werden, erfüllten sich jedoch nicht, obwohl er dort sowohl promoviert als auch habilitiert
worden war. Daher zeigte Christoffel nach einiger Zeit Interesse an anderen Positionen.
Und in der Tat wurde er, auf Empfehlung von
Leopold Kronecker (1823-1891) hin, an die 1872 neu
gegründete Kaiser-Wilhelm-Universität in Straßburg (heute Strasbourg in
Frankreich) berufen.
Am 12. März 1872 gab er schriftlich seinen Abschied von der Gewerbeakademie bekannt
und verließ diese gleich zum darauffolgenden Monatsersten.
Kossak wurde de facto sein Nachfolger, auch wenn er am 15. Januar 1873 zunächst nur
mit Wirkung zum 1. April des Jahres zum hauptberuflichen Lehrer ernannt wurde und
Titel und Position eines Professors an der Gewerbeakademie erst am 28. Mai 1875 erhielt.
Von 1876 bis 1879 hatte er auch einen Lehrauftrag für Mathematik an der Bauakademie inne.
Ab 1879 erübrigte sich diese nebenamtliche Tätigkeit, da in diesem Jahr,
wie bereits erwähnt, aus Bau- und Gewerbeakademie zusammen die TH Charlottenburg wurde,
in der Kossak weiter als Professor wirkte. Im akademischen Jahr 1883/84 bekleidete er dort
das Amt des Vorstands der „Abteilung V. für Allgemeine Wissenschaften“,
was in etwa der Position eines Dekans an einer Universität entsprach.
Der TH Charlottenburg blieb Kossak dann bis zu seinem Tod am 21. Januar 1892 treu.
Werk
Von seiner Promotion ab bis kurz nach dem Weggang Christoffels von der
Gewerbeakademie veröffentlichte Kossak mehrere Schriften:
- Das Additionstheorem der ultra-elliptischen Funktionen erster Ordnung, A. W. Schade's (L. Schade) Buchdruckerei, Stallschreiberstraße 47, Berlin, 1871 (als „Inaugural-Dissertation zur Erlangung des philosophischen Doctorgrades an der Georgia Augusta in Göttingen“) bzw. Nicolai'sche Verlagsbuchhandlung (A. Effert & L. Lindtner), Berlin, 1871
- Zur Theorie der elliptischen Transzendenten, Nicolai'sche Verlagsbuchhandlung (A. Effert & L. Lindtner), Berlin, 1872
- Die Elemente der Arithmetik. Programmabhandlung des Werderschen Gymnasiums in Berlin, Nicolai'sche Verlagsbuchhandlung (A. Effert & L. Lindtner), Berlin, 1872.
Die Publikationen über ultra-elliptische und elliptische Funktionen
Die erste Arbeit der obigen Liste ist Kossaks bereits erwähnte Dissertation,
und auch die zweite fällt in einen Bereich der Mathematik,
der sowohl für das Werk von Rosenhain als auch das von Weierstraß zentral war:
Bezeichnet P(t) ein Polynom in der Variablen t,
so lässt sich das Integral
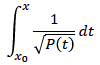
des Kehrwerts der Quadratwurzel von P(t) durch explizites Angeben
einer Stammfunktion bestimmen, wenn der Grad von P höchstens 2 beträgt.
Falls der Grad gleich 2 ist, kommt dabei die Arcus-Sinus-Funktion als Umkehrung
der Sinus-Funktion ins Spiel.
Der Fall, dass der Grad von P gleich 3 oder 4 ist,
umfasst den Spezialfall der Länge eines Ellipsenbogens,
weshalb hier von elliptischen Integralen gesprochen wird.
Niels Henrik Abel (1802-1829),
Carl Friedrich Gauß
(1777-1855) und
Carl Gustav Jacob Jacobi (1804-1851) hatten
in den Jahren um 1825 erkannt, dass die Umkehrfunktionen dieser Integrale, die sogenannten
elliptischen Funktionen, doppelt-periodische Funktionen einer komplexen
Veränderlichen sind, die sich mittels Quotienten von
Theta-Reihen darstellen
lassen, welche für alle Argumente konvergieren.
Den ersten Schritt zu einer Verallgemeinerung dieser prominenten Ergebnisse machten um 1846
Adolph Göpel (1812-1847) und
Rosenhain.
Unabhängig von einander gelang es ihnen, den Fall der ultra-elliptischen Funktionen
zu behandeln, bei dem P einen der beiden nächsthöheren Grade, 5 bzw. 6, besitzt.
Göpel, Bibliothekar an der Könglichen Bibliothek in Berlin, starb zwar kurz danach,
aber Rosenhain, übrigens ein Schüler Jacobis, der sehr viel von ihm hielt,
wurde im Jahr 1849 für seine Arbeit der 1845 für dieses Problem ausgelobte Preis der
Pariser Akademie verliehen.
Rosenhain hatte allerdings politische Schwierigkeiten wegen seiner demokratischen Aktivitäten
während der Revolution 1848/49 und musste daher die nächsten Jahre in Wien im Exil
verbringen.
Weierstraß hingegen veröffentlichte als Beilage zum
„Jahresbericht über das Gymnasium zu Braunsberg in dem Schuljahre 1848-1849“
eine Methode, um das allgemeine Problem zu behandeln, dass der Grad von P beliebig
groß sein kann.
In einem Artikel „Zur Theorie der Abel'schen Functionen“ in
Crelles Journal für die reine und angewandte Mathematik machte er seine Ideen 1854
bekannt und begründete damit seine akademische Karriere. Rosenhain jedoch erhielt zwar
1857 – offenbar unter Unterstützung durch
Gustav Leujeune Dirichlet (1805-1859) –
ein Extraordinariat an seiner Heimatuniversität Königsberg, konnte aber an seine alten
wissenschaftlichen Erfolge in der Mathematik nicht mehr anschließen.
In der 1. und der 2. Arbeit griff Kossak bezeichnenderweise nicht den Ansatz von
Weierstraß auf, sondern schloss sich an die Pariser Preisschrift von Rosenhain an:
Ähnlich, wie es für die Sinus-Funktion ein
Additionstheorem gibt,
existiert ein solches auch für elliptische Funktionen und
sogar für die von Rosenhain behandelten ultra-elliptischen Funktionen.
Kossak beschäftigte sich in seiner 1. Schrift mit verschiedenen Formen und
Herleitungsweisen dieses Theorems. In der 2. Arbeit hingegen griff er eine Idee Rosenhains
aus der Einleitung der genannten Preisschrift für den einfacheren Fall der elliptischen
Funktionen auf und arbeitete sie aus.
Die Publikation über den Weierstraß'schen Zahlbegriff
In der zweiten Hälfte des 19. Jahrhunderts wurde klar, dass viele der in der Analysis
verwendeten Schlüsse auf Eigenschaften des zu Grunde gelegten Zahlbereichs beruhen.
Als Folge davon wurden in den Jahren um 1870 zahlreiche Definitionen für die reellen Zahlen
vorgeschlagen, so von
Georg Cantor (1845-1918),
Richard Dedekind (1831-1916),
Eduard Heine (1821-1881) und
Charles Méray (1835-1911).
Auch Weierstraß stellte in seinem vier Semester umfassenden Vorlesungszyklus
regelmäßig solch eine Definition vor:
Er begann dabei mit einer „Einheit“ e,
die zunächst die Einheit einer Größe des täglichen Lebens sein konnte,
etwa eine Münze mit festem Wert, aber im Verlaufe der Betrachtungen
zumeist den Wert 1 oder auch i für die imaginäre Einheit erhielt.
Daneben betrachtete er noch für jede natürliche Zahl n
„genaue Teile“ e/n von e,
von denen jeweils n zusammengenommen die Einheit e ergeben. Exemplare der Einheit
e sowie von deren genauen Teilen e/n, für beliebiges
n, fasste er zu „Aggregaten“ zusammen.
(Modern formuliert, kann man diese als Multimengen auffassen,
in denen also Elemente mehrfach auftreten dürfen.)
Ein derartiges Aggregat aus nur endlich vielen Elementen definiert durch
Zusammenzählen dieser Elemente stets ein rationales Vielfaches von e.
Im Fall eines Aggregats aus unendlich vielen Elementen verlangte Weierstraß hingegen,
dass es eine feste Schranke gibt, so dass die Summe von je endlich vielen der Elemente
stets höchstens so groß wie diese Schranke ist;
in diesem Falle definiert das Aggregat ein positives reelles Vielfaches von e.
Um auch die negativen Vielfachen von e zu erfassen, führte Weierstraß eine
„entgegengesetzte“ Einheit e′ zu der gegebenen Einheit e ein,
die beim Zusammenziehen mit e den Wert 0 ergibt,
und führte eine entsprechende Konstruktion wie für die positiven
reellen Vielfachen von e auch für die Vielfachen von e′ durch,
was ihm die negativen reellen Vielfachen von e lieferte.
Beliebige reelle Vielfache wurden durch das Zusammenfügen eines positiven
mit einem negativen Vielfachen definiert.
Mit e:=+1 und e′:=−1 erhielt Weierstraß so die üblichen reellen Zahlen,
mit e:=+i und e′:=−i die rein imaginären Zahlen.
Durch Zusammennehmen von +1 und +i als Einheiten nebst ihren entgegengesetzten Einheiten
ergaben sich die üblichen komplexen Zahlen, die er für seine Theorie der analytischen,
elliptischen und Abel'schen Funktionen benötigte.
Daneben interessierte sich Weierstraß auch für die Frage,
inwieweit sich diese Konstruktion zu „hyper-komplexen Zahlen“ verallgemeinern
lässt; in moderner Sprache geht es dabei um die Klassifikation endlich-dimensionaler
reeller Algebren, etwa um den Nachweis, dass die komplexen Zahlen den einzigen
endlich-dimensionalen Erweiterungskörper der reellen Zahlen bilden.
Über seine Theorie des Zahlbegriffs veröffentlichte Weierstraß allerdings
nur eine einzige Arbeit – im Jahr 1884 über hyper-komplexe Zahlen.
Insbesondere über seine Konstruktion der irrationalen reellen Zahlen trug er nur in seinen
Vorlesungen vor; selbst in seinen Mathematischen Werken findet sich nichts dazu.
Daher blieb es anderen vorbehalten, seine Ergebnisse zu veröffentlichen.
Kossak war der erste, der dies in seiner 3. Arbeit (siehe obige Liste) aus dem Jahr 1872 tat,
die auf seinem Besuch der Weierstraß'schen Vorlesung
„Principien der Theorie der analytischen Functionen“ basierte.
(Nach ihm publizierten
Salvatore Pincherle [1853-1936]
im Jahr 1880,
Otto Biermann
[1858-1909] im Jahr 1887 und
Victor von Dantscher [1847-1921]
im Jahr 1908 Darstellungen über den Weierstraß'schen Zahlbegriff.)
Kossaks Publikation erfolgte in besonderer Form, die mit der
Humboldt'schen Bildungsreform zu tun hatte:
Mit dieser war der Anspruch verbunden, dass Gymnasiallehrer auch forschende Wissenschaftler seien.
Als Konsequenz davon mussten die als Broschüren gedruckten Schulprogramme,
mit denen Gymnasien jährlich über die zentralen Ereignisse des Schuljahres berichteten
bzw. diese ankündigten,
eine Programmabhandlung enthalten, eine wissenschaftliche Arbeit,
die einer der Lehrer der Schule verfasst hatte.
Da die Theorie des Zahlbegriffs auch für die Schule von Bedeutung ist,
bot es sich für Kossak somit an, seine Ausarbeitung der Weierstraß'schen
Ideen nicht als Zeitschriftenartikel oder als eigenständige Schrift zu veröffentlichen,
sondern im Rahmen des Schulprogramms des Werderschen Gymnasiums, an dem er tätig war
(siehe Fußnote 1).
Damit zielte er auf ein nicht-universitäres Publikum, was auch dadurch belegt wird,
dass er den innermathematischen Überlegungen eine ausführliche
„Historische Übersicht über die Entwickelung der Arithmetik“ voranstellte.
Es ist allerdings keinesfalls klar, inwieweit diese Arbeiten außerhalb der jeweiligen
Schule überhaupt wahrgenommen wurden:
Dirichlet etwa schrieb über die von Weierstraß im Jahr 1849 verfasste Programmabhandlung:
„H. Weierstraß, dessen seltenes Talent die Mathematiker schon vor 6 Jahren in einem
vortreffichen Schulprogramm hätten erkennen können,
wenn diese Schrift nicht leider ganz unbekannt geblieben wäre, […]“.
Im Gegensatz dazu wurde Kossaks Programmabhandlung umgehend beachtet,
auch wenn es Kritik war, die er sich damit einhandelte:
Am 20. Juni 1872 wies Hermann Amandus Schwarz,
der zu jener Zeit am Polytechnikum in Zürich wirkte,
seinen akademischen Lehrer Weierstraß auf diese Schrift hin,
insbesondere auf die Ungenauigkeiten und auch Fehler,
die Kossak bei der Diskussion der hyper-komplexen Zahlen unterlaufen waren.
Dessen Darstellung der Theorie der komplexen, insbesondere der irrationalen reellen Zahlen
hingegen hatte unter den kritischen Augen von Schwarz Bestand,
so dass man sie als korrekte Wiedergabe der Weierstraß'schen Gedanken ansehen kann!
(Weiterhin empfand Schwarz die Anmerkungen zur Geschichte des Zahlbegriffs als
überflüssig.)
Generell liest man allerdings zwischen den Zeilen, dass Schwarz vor allen Dingen
störte, dass Kossak Ergebnisse von Weierstraß veröffentlichte,
zwar unter Nennung von dessen Namen, aber dies wohl eher,
um seinen Ausführungen mehr Gewicht zu verleihen – und dies,
obwohl Kossak eben nicht als Schüler von Weierstraß anzusehen ist.
Möglicherweise war es auch mehr dieses generelle Unbehagen,
das Weierstraß selbst dazu brachte, sich am 5. April 1885 in einem Brief an
Gösta
Mittag-Leffler (1846-1927) zu beklagen, Kossak habe seine Theorie „verhunzt“.
Waren die bislang zitierten Kritiken an Kossak zunächst nur jeweils brieflich an eine
Person gerichtet und wurden erst nach dem Tod der handelnden Personen von Dritten publiziert,
so machte
Gottlob Frege (1848-1925)
seine Kritik an Kossaks Darstellung bereits 1884 in seinem Buch
„Die Grundlagen der Arithmetik“ öffentlich.
Er stellte darin zum Beispiel die Frage,
wie man zu einer beliebigen gegebenen Einheit e stets die entgegengesetzte
e′ finden will oder gar die zugehörige imaginäre Einheit,
deren Quadrat gleich der entgegensetzten Einheit e′ ist.
Allerdings nannte er dabei zwar Kossak als Autor,
meinte jedoch in Wirklichkeit die Überlegungen von Weierstraß.
Dies machte er jedoch erst im Band II seiner „Grundgesetze der Arithmetik“
von 1903 deutlich, wo er auch andere Darstellungen der Weierstraß'schen Theorie
der Zahlen als Quellen heranzog.
Referenzen
| [1] | Eberhard Knobloch: Mathematik an der Technischen Hochschule und der Technischen Universität Berlin 1770 – 1988, Verlag für Wissenschafts- und Regionalgeschichte Dr. Martin Engel, Berlin, 1998 | |
| [2] | Emil Lampe: Ernst Kossak. Nachruf, gesprochen bei der Begräbnisfeier in der Aula der Technischen Hochschule zu Charlottenburg am 25. Januar 1892, Jahresbericht der Deutschen Mathematiker-Vereinigung 12 (1903), S. 500-504. | |
| [3] | Gert Schubring: Analysen der Profile der Mathematik-Schulprogramme in den verschiedenen deutschen Staaten des 19. Jahrhunderts, in: Norman Ächtler (Hrsg.): Schulprogramme Höherer Lehranstalten. Interdisziplinäre Perspektiven auf eine wiederentdeckte bildungs- und kulturwissenschaftliche Quellengattung, Wehrhahn, Hannover, 2021, S. 305-327. | |
| [4] | Zur Promotion Ernst Kossaks: Niedersächsische Staats- und Universitätsbibliothek Göttingen, Universitätsarchiv Göttingen, Philosophische Fakultät 156, S. 414-418 und 157, S. 12-13 |
Bildnachweis
| Porträt | aus Reinhard Bölling: Das Fotoalbum für Weierstraß – A Photo Album for Weierstrass, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig / Wiesbaden 1994, Foto 24.7., Foto: Hugo Danz, Berlin, Quelle: https://smb.museum-digital.de/object/68184 Lizenz/Verwendung gemäß CC BY NC SA 3.0 @ Kunstbibliothek / Staatliche Museen zu Berlin – Preußischer Kulturbesitz, das Bild ist angemessen zugeschnitten |
1) Inwieweit das Friedrichswerdersche
Gymnasium auch als Werdersches Gymnasium genannt wurde, wird sich nicht auf
einfache Weise klären lassen. Fest steht allerdings, dass Kossaks Abhandlung
„Die Elemente der Arithmetik“ auf dem Titelblatt als
„Programmabhandlung des Werderschen Gymnasiums“ bezeichnet wird.
2) Zur Begrifflichkeit siehe den
Wikipedia-Artikel zum
Bildungssystem in Deutschland.
